Lab 5 - R Code#
Authors: Valerie Dube, Erzo Garay, Juan Marcos Guerrero y Matias Villalba
Replication and Data analysis#
library(hdm)
library(xtable)
library(randomForest)
library(glmnet)
library(sandwich)
library(rpart)
library(nnet)
library(gbm)
library(rpart.plot)
library(keras)
library(xtable)
library(glmnet)
library(randomForest)
library(ggplot2)
randomForest 4.7-1.1
Type rfNews() to see new features/changes/bug fixes.
Loading required package: Matrix
Loaded glmnet 4.1-8
Loaded gbm 2.2.2
This version of gbm is no longer under development. Consider transitioning to gbm3, https://github.com/gbm-developers/gbm3
Attaching package: 'ggplot2'
The following object is masked from 'package:randomForest':
margin
set.seed(1)
rm(list = ls())
library(ggplot2)
library(WeightIt)
library(cobalt)
cobalt (Version 4.5.5, Build Date: 2024-04-02)
1. Descriptives#
1.1. Descriptive table (vale)#
# Import data and see first observations
data = read.csv("../../data/processed_esti.csv")
head(data)
| y | w | gender_female | gender_male | gender_transgender | ethnicgrp_asian | ethnicgrp_black | ethnicgrp_mixed_multiple | ethnicgrp_other | ethnicgrp_white | partners1 | postlaunch | msm | age | imd_decile | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 27 | 5 |
| 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 19 | 6 |
| 3 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 26 | 4 |
| 4 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 20 | 2 |
| 5 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 24 | 3 |
| 6 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 24 | 2 |
str(data)
'data.frame': 1739 obs. of 15 variables:
$ y : int 1 0 0 0 1 1 1 0 0 1 ...
$ w : int 1 0 1 0 1 1 1 0 1 1 ...
$ gender_female : int 0 0 0 1 1 0 1 0 0 1 ...
$ gender_male : int 1 1 1 0 0 1 0 1 1 0 ...
$ gender_transgender : int 0 0 0 0 0 0 0 0 0 0 ...
$ ethnicgrp_asian : int 0 0 0 0 1 0 0 0 0 0 ...
$ ethnicgrp_black : int 0 0 1 0 0 0 0 1 0 1 ...
$ ethnicgrp_mixed_multiple: int 1 0 0 0 0 0 0 0 0 0 ...
$ ethnicgrp_other : int 0 0 0 0 0 0 0 0 0 0 ...
$ ethnicgrp_white : int 0 1 0 1 0 1 1 0 1 0 ...
$ partners1 : int 0 0 0 1 0 0 0 0 1 0 ...
$ postlaunch : int 1 0 1 0 1 1 0 1 0 0 ...
$ msm : int 0 0 0 0 0 0 0 0 0 0 ...
$ age : int 27 19 26 20 24 24 24 21 27 21 ...
$ imd_decile : int 5 6 4 2 3 2 4 2 2 6 ...
by(data[, !names(data) %in% 'y'], data$w, summary)
data$w: 0
w gender_female gender_male gender_transgender
Min. :0 Min. :0.0000 Min. :0.0000 Min. :0.000000
1st Qu.:0 1st Qu.:0.0000 1st Qu.:0.0000 1st Qu.:0.000000
Median :0 Median :1.0000 Median :0.0000 Median :0.000000
Mean :0 Mean :0.5807 Mean :0.4181 Mean :0.001223
3rd Qu.:0 3rd Qu.:1.0000 3rd Qu.:1.0000 3rd Qu.:0.000000
Max. :0 Max. :1.0000 Max. :1.0000 Max. :1.000000
ethnicgrp_asian ethnicgrp_black ethnicgrp_mixed_multiple ethnicgrp_other
Min. :0.00000 Min. :0.00000 Min. :0.00000 Min. :0.00000
1st Qu.:0.00000 1st Qu.:0.00000 1st Qu.:0.00000 1st Qu.:0.00000
Median :0.00000 Median :0.00000 Median :0.00000 Median :0.00000
Mean :0.05501 Mean :0.09291 Mean :0.09291 Mean :0.01711
3rd Qu.:0.00000 3rd Qu.:0.00000 3rd Qu.:0.00000 3rd Qu.:0.00000
Max. :1.00000 Max. :1.00000 Max. :1.00000 Max. :1.00000
ethnicgrp_white partners1 postlaunch msm
Min. :0.0000 Min. :0.0000 Min. :0.0000 Min. :0.0000
1st Qu.:0.0000 1st Qu.:0.0000 1st Qu.:0.0000 1st Qu.:0.0000
Median :1.0000 Median :0.0000 Median :0.0000 Median :0.0000
Mean :0.7421 Mean :0.2922 Mean :0.4731 Mean :0.1381
3rd Qu.:1.0000 3rd Qu.:1.0000 3rd Qu.:1.0000 3rd Qu.:0.0000
Max. :1.0000 Max. :1.0000 Max. :1.0000 Max. :1.0000
age imd_decile
Min. :16.00 Min. :1.000
1st Qu.:20.00 1st Qu.:2.000
Median :23.00 Median :3.000
Mean :23.05 Mean :3.484
3rd Qu.:26.00 3rd Qu.:4.000
Max. :30.00 Max. :9.000
------------------------------------------------------------
data$w: 1
w gender_female gender_male gender_transgender
Min. :1 Min. :0.0000 Min. :0.0000 Min. :0.000000
1st Qu.:1 1st Qu.:0.0000 1st Qu.:0.0000 1st Qu.:0.000000
Median :1 Median :1.0000 Median :0.0000 Median :0.000000
Mean :1 Mean :0.5874 Mean :0.4093 Mean :0.003257
3rd Qu.:1 3rd Qu.:1.0000 3rd Qu.:1.0000 3rd Qu.:0.000000
Max. :1 Max. :1.0000 Max. :1.0000 Max. :1.000000
ethnicgrp_asian ethnicgrp_black ethnicgrp_mixed_multiple
Min. :0.00000 Min. :0.00000 Min. :0.00000
1st Qu.:0.00000 1st Qu.:0.00000 1st Qu.:0.00000
Median :0.00000 Median :0.00000 Median :0.00000
Mean :0.07166 Mean :0.08035 Mean :0.08469
3rd Qu.:0.00000 3rd Qu.:0.00000 3rd Qu.:0.00000
Max. :1.00000 Max. :1.00000 Max. :1.00000
ethnicgrp_other ethnicgrp_white partners1 postlaunch
Min. :0.000000 Min. :0.0000 Min. :0.0000 Min. :0.0000
1st Qu.:0.000000 1st Qu.:1.0000 1st Qu.:0.0000 1st Qu.:0.0000
Median :0.000000 Median :1.0000 Median :0.0000 Median :1.0000
Mean :0.009772 Mean :0.7535 Mean :0.3008 Mean :0.5559
3rd Qu.:0.000000 3rd Qu.:1.0000 3rd Qu.:1.0000 3rd Qu.:1.0000
Max. :1.000000 Max. :1.0000 Max. :1.0000 Max. :1.0000
msm age imd_decile
Min. :0.0000 Min. :16.00 Min. :1.00
1st Qu.:0.0000 1st Qu.:20.00 1st Qu.:2.00
Median :0.0000 Median :23.00 Median :3.00
Mean :0.1238 Mean :23.16 Mean :3.46
3rd Qu.:0.0000 3rd Qu.:26.00 3rd Qu.:4.00
Max. :1.0000 Max. :30.00 Max. :9.00
The observations for each variable are generally balanced between the control and treatment groups. Additionally, most participants are white, with an average age of approximately 23. The mean IMD decile scores are around 3.5, indicating that participants in both groups tend to come from more deprived areas.
1.2. Descriptive graphs (vale)#
#Generating propensity score weights for the ATT
w.out <- WeightIt::weightit(w ~ age + gender_male + ethnicgrp_white + partners1 + imd_decile,
data = data,
method = "glm",
estimand = "ATT")
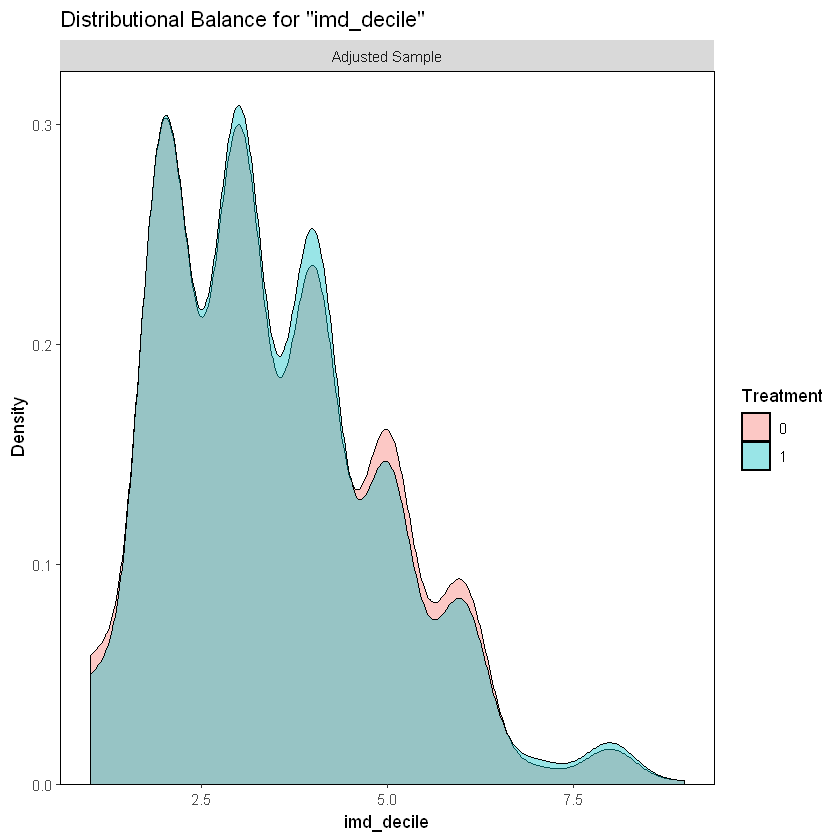
bal.tab(w.out)
Balance Measures
Type Diff.Adj
prop.score Distance -0.0025
age Contin. -0.0009
gender_male Binary 0.0004
ethnicgrp_white Binary -0.0001
partners1 Binary -0.0010
imd_decile Contin. 0.0021
Effective sample sizes
Control Treated
Unadjusted 818. 921
Adjusted 815.66 921
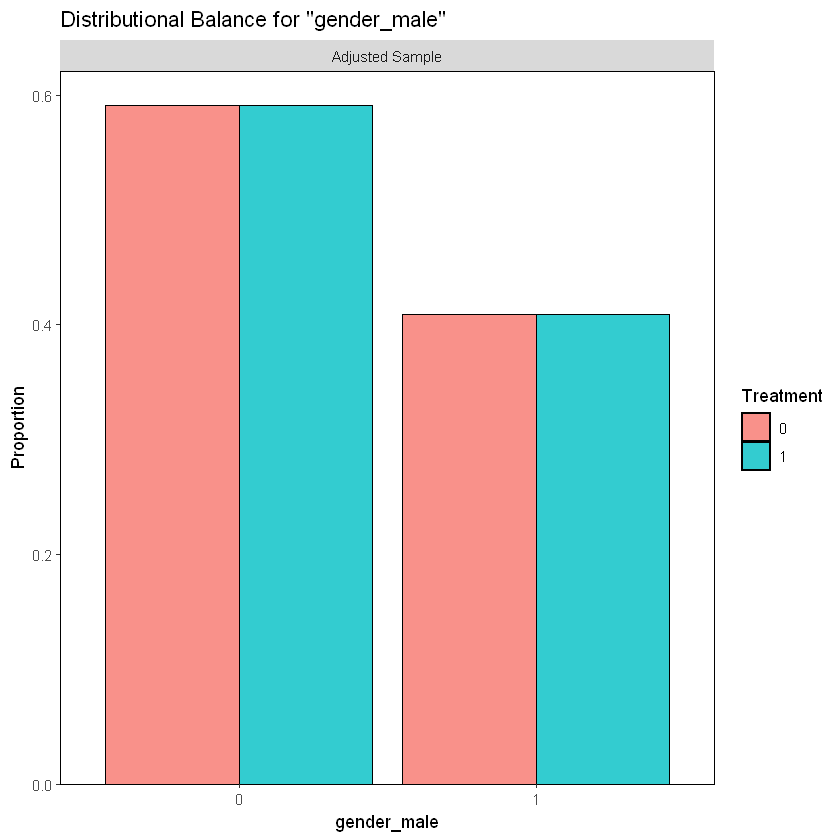
As we saw in section 1.1., there is a similar percentage of males and females participants in each treatment group in the sample.
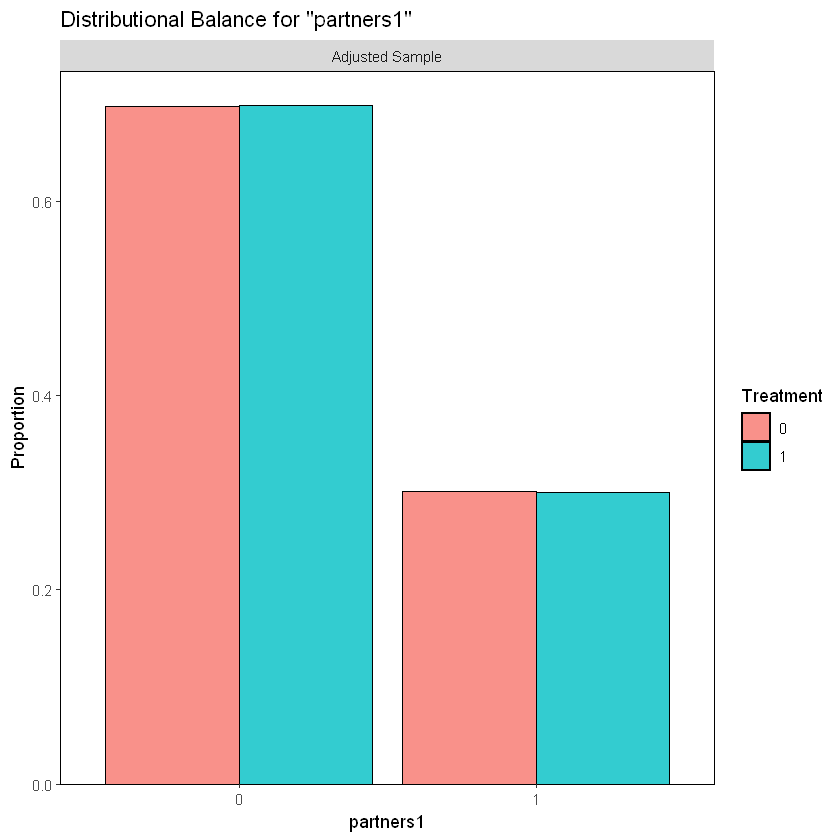
In a similar manner, we note an equal percentage of participants with 2 or more sexual partners as well as those with 1 sexual partner in the last 12 months from the beginning of the study, per treatment or control group.
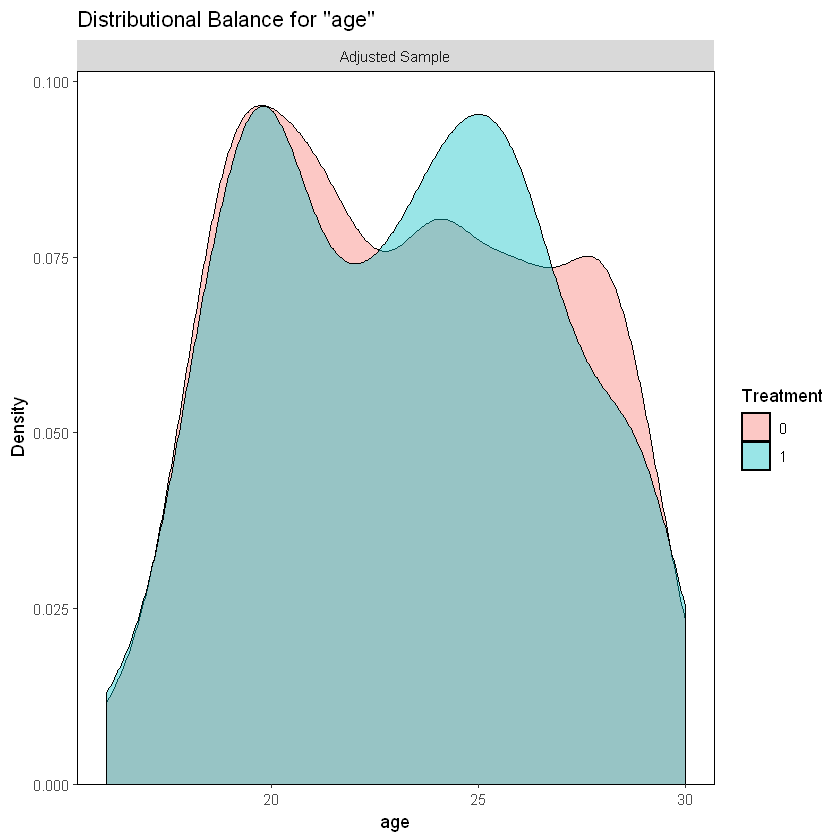
We can see a higher percentage of participants aged between 23 and 27 in the treatment group. Also, there is a higher perceptange of participants aged between 21 and 22 and 27 and 29 in the control group.
In the case of the IMD decile, an index that measures poverty in the UK, we can see the same proportion of participants in each group.
2. Linear Regression analysis#
2.1. Regression 1: \(y = \beta_0 + \beta_1 T + \epsilon\) (Vale)#
lm(formula = y ~ w, data = data)
Call:
lm(formula = y ~ w, data = data)
Coefficients:
(Intercept) w
0.2115 0.2652
We found that the adjusted R-squared is 0.076 and the ATE is approximately 0.27. This means that the treatment explains only 7.6% of the increase in the STI tests between the control and treatment groups. Additionally, receiving the treatment (i.e. being invited to use the internet-based sexual health service) increases, on average, the probability of taking an STI test by 26.5%.
2.2. Regression 2: \(y = \beta_0 + \beta_1 T + \beta_2 X + \epsilon\) (vale)#
lm(formula = y ~ w + age + gender_female + ethnicgrp_white + ethnicgrp_black + ethnicgrp_mixed_multiple + partners1 + postlaunch + imd_decile + msm, data = data)
Call:
lm(formula = y ~ w + age + gender_female + ethnicgrp_white +
ethnicgrp_black + ethnicgrp_mixed_multiple + partners1 +
postlaunch + imd_decile + msm, data = data)
Coefficients:
(Intercept) w age
-0.162682 0.255716 0.012476
gender_female ethnicgrp_white ethnicgrp_black
0.091026 0.049819 -0.040238
ethnicgrp_mixed_multiple partners1 postlaunch
-0.035933 -0.059428 0.077319
imd_decile msm
-0.004155 -0.006273
Compared to the previous regression, when we include additional variables (age, gender, ethnic group, number of sexual partners, the indicator for Randomised after SH:24 made publicly available, the indicator for men who have sex with men, and the socioeconomic level measured by deciles), we observe an increase in the adjusted R-squared of approximately 0.3 percentage points (from 0.1). Additionally, the ATE decreases by 0.003 percentage points, indicating a negative bias.
It is worth mentioning that we omit gender_male to avoid collinearity with gender_female. Similarly, we exclude the less relevant ethnic group (i.e. the one with fewer observations) to prevent the same issue.
2.3.#
We observe that the ATE using double lasso is akin to the OLS with confounders, along with the adjusted R-squared.
2.4.#
In general, the three ATEs are very similar, but we consider that the models that include the cofounders (OLS with controls and DL) are better estimated.
3. Non-Linear Methods DML#
rm(list=ls())
DML <- as.data.frame(read.table("../../../data/processed_esti.csv", header=T ,sep=","))
#DML <- as.data.frame(read.table("C:/Users/Erzo/Documents/GitHub/CausalAI-Course/data/processed_esti.csv", header=T ,sep=","))
set.seed(1234)
training <- sample(nrow(DML), nrow(DML)*(3/4), replace=FALSE)
data_train <- DML[training,]
data_test <- DML[-training,]
Y_test <- data_test$y
y = as.matrix(data_train[,1]) # outcome: growth rate
d = as.matrix(data_train[,2]) # treatment: initial wealth
x = as.matrix(data_train[,-c(1,2)]) # controls: country characteristics
Warning message in file(file, "rt"):
"cannot open file '../../../data/processed_esti.csv': No such file or directory"
Error in file(file, "rt"): cannot open the connection
Traceback:
1. as.data.frame(read.table("../../../data/processed_esti.csv",
. header = T, sep = ","))
2. read.table("../../../data/processed_esti.csv", header = T, sep = ",")
3. file(file, "rt")
DML function for Regression tree#
DML2.for.PLM.tree <- function(data_train, dreg, yreg, nfold=10) {
nobs <- nrow(data_train) #number of observations
foldid <- rep.int(1:nfold,times = ceiling(nobs/nfold))[sample.int(nobs)] #define folds indices
I <- split(1:nobs, foldid) #split observation indices into folds
ytil <- dtil <- rep(NA, nobs)
cat("fold: ")
for(b in 1:length(I)){
datitanow=data_train[-I[[b]],-c(2)]
datitanoy=data_train[-I[[b]],-c(1)]
datitanowpredict=data_train[I[[b]],-c(2)]
datitanoypredict=data_train[I[[b]],-c(1)]
dfit <- dreg(datitanoy) #take a fold out
yfit <- yreg(datitanow) # take a foldt out
dhat <- predict(dfit, datitanoypredict ) #predict the left-out fold
yhat <- predict(yfit, datitanowpredict ) #predict the left-out fold
dtil[I[[b]]] <- (d[I[[b]]] - dhat) #record residual for the left-out fold
ytil[I[[b]]] <- (y[I[[b]]] - yhat) #record residial for the left-out fold
cat(b," ")
}
rfit <- lm(ytil ~ dtil) #estimate the main parameter by regressing one residual on the other
coef.est <- coef(rfit)[2] #extract coefficient
se <- sqrt(vcovHC(rfit)[2,2]) #record robust standard error
cat(sprintf("\ncoef (se) = %g (%g)\n", coef.est , se)) #printing output
return( list(coef.est =coef.est , se=se, dtil=dtil, ytil=ytil) ) #save output and residuals
}
DML function for Boosting Trees#
DML2.for.PLM.boosttree <- function(data_train, dreg, yreg, nfold=10) {
nobs <- nrow(data_train) #number of observations
foldid <- rep.int(1:nfold,times = ceiling(nobs/nfold))[sample.int(nobs)] #define folds indices
I <- split(1:nobs, foldid) #split observation indices into folds
ytil <- dtil <- rep(NA, nobs)
cat("fold: ")
for(b in 1:length(I)){
datitanow=data_train[-I[[b]],-c(2)]
datitanoy=data_train[-I[[b]],-c(1)]
datitanowpredict=data_train[I[[b]],-c(2)]
datitanoypredict=data_train[I[[b]],-c(1)]
dfit <- dreg(datitanoy) #take a fold out
best.boostt <- gbm.perf(dfit, plot.it = FALSE) # cross-validation to determine when to stop
yfit <- yreg(datitanow) # take a foldt out
best.boosty <- gbm.perf(yfit, plot.it = FALSE) # cross-validation to determine when to stop
dhat <- predict(dfit, datitanoypredict, n.trees=best.boostt)
yhat <- predict(yfit, datitanowpredict, n.trees=best.boosty) #predict the left-out fold
dtil[I[[b]]] <- (d[I[[b]]] - dhat) #record residual for the left-out fold
ytil[I[[b]]] <- (y[I[[b]]] - yhat) #record residial for the left-out fold
cat(b," ")
}
rfit <- lm(ytil ~ dtil) #estimate the main parameter by regressing one residual on the other
coef.est <- coef(rfit)[2] #extract coefficient
se <- sqrt(vcovHC(rfit)[2,2]) #record robust standard error
cat(sprintf("\ncoef (se) = %g (%g)\n", coef.est , se)) #printing output
return( list(coef.est =coef.est , se=se, dtil=dtil, ytil=ytil) ) #save output and residuals
}
DML function for Lasso and Random Forest#
DML2.for.PLM <- function(x, d, y, dreg, yreg, nfold=10) {
nobs <- nrow(x) #number of observations
foldid <- rep.int(1:nfold,times = ceiling(nobs/nfold))[sample.int(nobs)] #define folds indices
I <- split(1:nobs, foldid) #split observation indices into folds
ytil <- dtil <- rep(NA, nobs)
cat("fold: ")
for(b in 1:length(I)){
dfit <- dreg(x[-I[[b]],], d[-I[[b]]]) #take a fold out
yfit <- yreg(x[-I[[b]],], y[-I[[b]]]) # take a foldt out
dhat <- predict(dfit, x[I[[b]],], type="response") #predict the left-out fold
yhat <- predict(yfit, x[I[[b]],], type="response") #predict the left-out fold
dtil[I[[b]]] <- (d[I[[b]]] - dhat) #record residual for the left-out fold
ytil[I[[b]]] <- (y[I[[b]]] - yhat) #record residial for the left-out fold
cat(b," ")
}
rfit <- lm(ytil ~ dtil) #estimate the main parameter by regressing one residual on the other
coef.est <- coef(rfit)[2] #extract coefficient
se <- sqrt(vcovHC(rfit)[2,2]) #record robust standard error
cat(sprintf("\ncoef (se) = %g (%g)\n", coef.est , se)) #printing output
return( list(coef.est =coef.est , se=se, dtil=dtil, ytil=ytil) ) #save output and residuals
}
3.1. Lasso#
cat(sprintf("\nDML with Lasso \n"))
dreg_lasso <- function(x,d){ rlasso(x,d, post=FALSE) } #ML method= lasso from hdm
yreg_lasso <- function(x,y){ rlasso(x,y, post=FALSE) } #ML method = lasso from hdm
DML2.lasso = DML2.for.PLM(x, d, y, dreg_lasso, yreg_lasso, nfold=10)
coef_lasso<-as.numeric(DML2.lasso$coef.est)
se_lasso<-as.numeric(DML2.lasso$se)
prRes_lassoD<- c(mean((DML2.lasso$dtil)^2));
prRes_lassoY<- c(mean((DML2.lasso$ytil)^2));
prRes_lasso<- rbind(coef_lasso,se_lasso,sqrt(prRes_lassoD), sqrt(prRes_lassoY));
rownames(prRes_lasso)<- c("Estimate","Standard Error","RMSE D", "RMSE Y");
colnames(prRes_lasso)<- c("Lasso")
prRes_lasso
DML with Lasso
fold:
Error in rlasso(x, d, post = FALSE): no se pudo encontrar la función "rlasso"
Traceback:
1. DML2.for.PLM(x, d, y, dreg_lasso, yreg_lasso, nfold = 10)
2. dreg(x[-I[[b]], ], d[-I[[b]]]) # at line 8 of file <text>
The message treatment providing information about Internet-accessed sexually transmitted infection testing predicts an increase in the probability that a person will get tested by 25.13 percentage points compared to receiving information about nearby clinics offering in-person testing. By providing both groups with information about testing, we mitigate the potential reminder effect, as both groups are equally prompted to consider testing. This approach allows us to isolate the impact of the type of information “Internet-accessed testing” versus “in-person clinic testing” on the likelihood of getting tested. Through randomized assignment, we establish causality rather than mere correlation, confirming that the intervention’s effect is driven by the unique advantages of Internet-accessed testing, such as increased privacy, reduced embarrassment, and convenience
3.2. Regression Trees#
# Tree
X_basic <- "gender_transgender + ethnicgrp_asian + ethnicgrp_black + ethnicgrp_mixed_multiple+ ethnicgrp_other + ethnicgrp_white + partners1 + postlaunch + msm + age+ imd_decile"
y_form_tree <- as.formula(paste("y", "~", X_basic))
t_form_tree <- as.formula(paste("w", "~", X_basic))
yreg_tree <- function(dataa){rpart(y_form_tree, dataa, minbucket=5, cp = 0.001)}
treg_tree <- function(dataa){rpart(t_form_tree, dataa, minbucket=5, cp = 0.001)}
DML2.tree = DML2.for.PLM.tree(data_train, treg_tree, yreg_tree, nfold=10)
coef_tree<-as.numeric(DML2.tree$coef.est)
se_tree<-as.numeric(DML2.tree$se)
prRes_treeD<- c(mean((DML2.tree$dtil)^2));
prRes_treeY<- c(mean((DML2.tree$ytil)^2));
prRes_tree<- rbind(coef_tree,se_tree,sqrt(prRes_treeD), sqrt(prRes_treeY));
rownames(prRes_tree)<- c("Estimate","Standard Error","RMSE D", "RMSE Y");
colnames(prRes_tree)<- c("Regression Tree")
prRes_tree
The message treatment providing information about Internet-accessed sexually transmitted infection testing predicts an increase in the probability that a person will get tested by 23.08 percentage points compared to receiving information about nearby clinics offering in-person testing. By providing both groups with information about testing, we mitigate the potential reminder effect, as both groups are equally prompted to consider testing. This approach allows us to isolate the impact of the type of information “Internet-accessed testing” versus “in-person clinic testing” on the likelihood of getting tested. Through randomized assignment, we establish causality rather than mere correlation, confirming that the intervention’s effect is driven by the unique advantages of Internet-accessed testing, such as increased privacy, reduced embarrassment, and convenience
3.3. Boosting Trees#
yreg_treeboost<- function(dataa){gbm(y_form_tree, data=dataa, distribution= "gaussian", bag.fraction = .5, interaction.depth=2, n.trees=1000, shrinkage=.01)}
treg_treeboost<- function(dataa){gbm(t_form_tree, data=dataa, distribution= "gaussian", bag.fraction = .5, interaction.depth=2, n.trees=1000, shrinkage=.01)}
DML2.boosttree = DML2.for.PLM.boosttree(data_train, treg_treeboost, yreg_treeboost, nfold=10)
coef_boosttree<-as.numeric(DML2.boosttree$coef.est)
se_boosttree<-as.numeric(DML2.boosttree$se)
prRes_boosttreeD<- c(mean((DML2.boosttree$dtil)^2));
prRes_boosttreeY<- c(mean((DML2.boosttree$ytil)^2));
prRes_boosttree<- rbind(coef_boosttree,se_boosttree,sqrt(prRes_boosttreeD), sqrt(prRes_boosttreeY));
rownames(prRes_boosttree)<- c("Estimate","Standard Error","RMSE D", "RMSE Y");
colnames(prRes_boosttree)<- c("Regression Tree")
prRes_boosttree
The message treatment providing information about Internet-accessed sexually transmitted infection testing predicts an increase in the probability that a person will get tested by 25.28 percentage points compared to receiving information about nearby clinics offering in-person testing. By providing both groups with information about testing, we mitigate the potential reminder effect, as both groups are equally prompted to consider testing. This approach allows us to isolate the impact of the type of information “Internet-accessed testing” versus “in-person clinic testing” on the likelihood of getting tested. Through randomized assignment, we establish causality rather than mere correlation, confirming that the intervention’s effect is driven by the unique advantages of Internet-accessed testing, such as increased privacy, reduced embarrassment, and convenience
3.4. Random Forest#
cat(sprintf("\nDML with Random Forest \n"))
dreg <- function(x,d){ randomForest(x, d) } #ML method=Forest
yreg <- function(x,y){ randomForest(x, y) } #ML method=Forest
DML2.RF = DML2.for.PLM(x, d, y, dreg, yreg, nfold=10)
coef_RF<-as.numeric(DML2.RF$coef.est)
se_RF<-as.numeric(DML2.RF$se)
prRes_RFD<- c(mean((DML2.RF$dtil)^2));
prRes_RFY<- c(mean((DML2.RF$ytil)^2));
prRes_RF<- rbind(coef_RF,se_RF,sqrt(prRes_RFD), sqrt(prRes_RFY));
rownames(prRes_RF)<- c("Estimate","Standard Error","RMSE D", "RMSE Y");
colnames(prRes_RF)<- c("Random Forest")
prRes_RF
The message treatment providing information about Internet-accessed sexually transmitted infection testing predicts an increase in the probability that a person will get tested by 24.14 percentage points compared to receiving information about nearby clinics offering in-person testing. By providing both groups with information about testing, we mitigate the potential reminder effect, as both groups are equally prompted to consider testing. This approach allows us to isolate the impact of the type of information “Internet-accessed testing” versus “in-person clinic testing” on the likelihood of getting tested. Through randomized assignment, we establish causality rather than mere correlation, confirming that the intervention’s effect is driven by the unique advantages of Internet-accessed testing, such as increased privacy, reduced embarrassment, and convenience
3.5. Table and Coefficient plot#
Table#
prRes.D<- c( mean((DML2.lasso$dtil)^2), mean((DML2.tree$dtil)^2), mean((DML2.boosttree$dtil)^2), mean((DML2.RF$dtil)^2));
prRes.Y<- c(mean((DML2.lasso$ytil)^2), mean((DML2.tree$ytil)^2),mean((DML2.boosttree$ytil)^2),mean((DML2.RF$ytil)^2));
prRes<- rbind(sqrt(prRes.D), sqrt(prRes.Y));
rownames(prRes)<- c("RMSE D", "RMSE Y");
colnames(prRes)<- c("Lasso", "Reg Tree", "Boost Tree", "Random Forest")
table <- matrix(0,4,4)
# Point Estimate
table[1,1] <- as.numeric(DML2.lasso$coef.est)
table[2,1] <- as.numeric(DML2.tree$coef.est)
table[3,1] <- as.numeric(DML2.boosttree$coef.est)
table[4,1] <- as.numeric(DML2.RF$coef.est)
# SE
table[1,2] <- as.numeric(DML2.lasso$se)
table[2,2] <- as.numeric(DML2.tree$se)
table[3,2] <- as.numeric(DML2.boosttree$se)
table[4,2] <- as.numeric(DML2.RF$se)
# RMSE Y
table[1,3] <- as.numeric(prRes[2,1])
table[2,3] <- as.numeric(prRes[2,2])
table[3,3] <- as.numeric(prRes[2,3])
table[4,3] <- as.numeric(prRes[2,4])
# RMSE D
table[1,4] <- as.numeric(prRes[1,1])
table[2,4] <- as.numeric(prRes[1,2])
table[3,4] <- as.numeric(prRes[1,3])
table[4,4] <- as.numeric(prRes[1,4])
# print results
colnames(table) <- c("Estimate","Standard Error", "RMSE Y", "RMSE D")
rownames(table) <- c("Lasso", "Reg Tree", "Boost Tree", "Random Forest")
table
Coefficient Plot#
table_ci<-as.data.frame(table)
table_ci$CI_Lower_1 <- table_ci$Estimate - 2.576 * table_ci$'Standard Error'
table_ci$CI_Upper_1 <- table_ci$Estimate + 2.576 * table_ci$'Standard Error'
table_ci$CI_Lower_5 <- table_ci$Estimate - 1.96 * table_ci$'Standard Error'
table_ci$CI_Upper_5 <- table_ci$Estimate + 1.96 * table_ci$'Standard Error'
table_ci$CI_Lower_10 <- table_ci$Estimate - 1.645 * table_ci$'Standard Error'
table_ci$CI_Upper_10 <- table_ci$Estimate + 1.645 * table_ci$'Standard Error'
ggplot(table_ci, aes(x = rownames(table_ci), y = Estimate)) +
geom_point(size = 4) +
geom_errorbar(aes(ymin = CI_Lower_5, ymax = CI_Upper_5), width = 0.2, color = "blue", alpha = 0.7) +
geom_errorbar(aes(ymin = CI_Lower_10, ymax = CI_Upper_10), width = 0.1, color = "red", alpha = 0.7) +
geom_errorbar(aes(ymin = CI_Lower_1, ymax = CI_Upper_1), width = 0.05, color = "green", alpha = 0.7) +
labs(title = "Estimated Coefficients with Confidence Intervals",
y = "Estimate",
x = "Method") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))
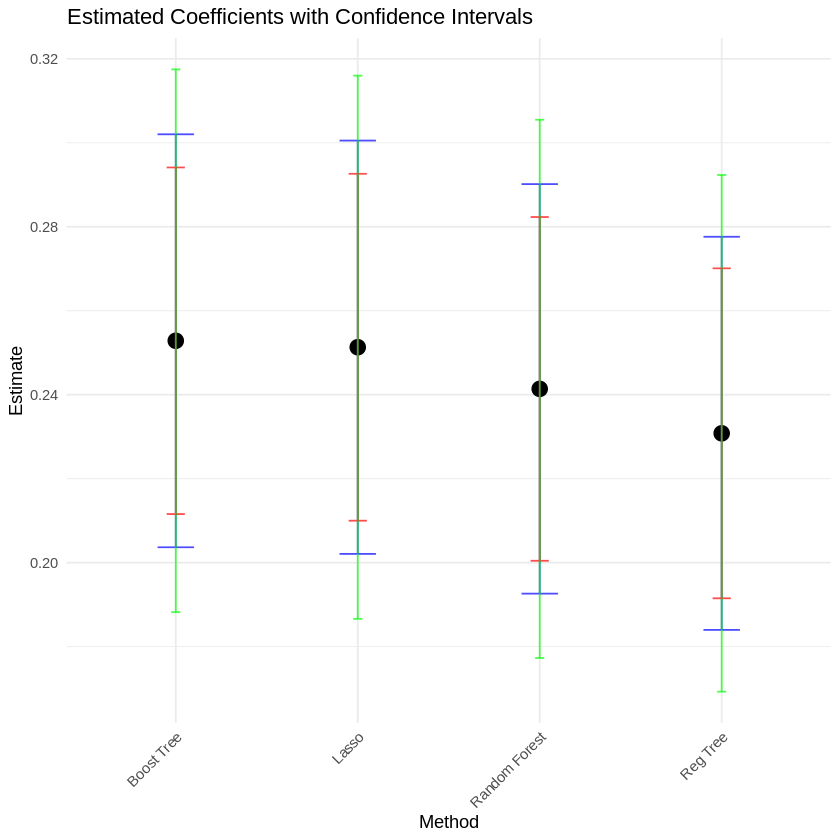
3.6. Model#
To choose the best model, we must compare the RMSEs of the outcome variable Y. In this case, the model with the lowest RMSE for Y is generated by Lasso (0.4716420), whereas the lowest for the treatment is generated by Boosting Trees (0.4983734). Therefore, DML could be employed with Y cleaned using Lasso and the treatment using Boosting Trees.