Lab 3 - Julia Code#
Group 3: Valerie Dube, Erzo Garay, Juan Marcos Guerrero y Matías Villalba,
1. Neyman Orthogonality Proof#
\(Y_{nx1}=\alpha D_{nx1}+W_{nxp}\beta_{px1}+\epsilon_{nx1}\\ \widetilde{Y}_{nx1}=Y_{nx1}-W_{nxp}X_{{{Yw}_{px1}}}\\ \widetilde{D}_{nx1}=D_{nx1}-W_{nxp}X_{{{Dw}_{px1}}}\\ W=Matrix\ composed\ by\ one\ variable\ in\ each\ column\\ X=Vector\ of\ coefficients\\ n=N° observations\\ p=N° confounders \\\ \\\ \\\ M(a,\eta)=E[(\widetilde{Y}_{nx1}(\eta_{1})-a\widetilde{D}(\eta_{2})_{nx1})'(\widetilde{D}(\eta_{2})_{nx1})]=0\\ \frac{\partial a}{\partial \eta}=-[\frac{\partial M}{\partial a}(\alpha,\eta_{0})]^{-1}[\frac{\partial M}{\partial \eta}(\alpha,\eta_{0})]\\ \frac{\partial M}{\partial \eta}(\alpha,\eta_{0})=\frac{\partial M}{\partial \eta_{1}}(\alpha,X_{Yw},X_{Dw})+\frac{\partial M}{\partial \eta_{2}}(\alpha,X_{Yw},X_{Dw})\\ S_{1}=\frac{\partial M}{\partial \eta_{1}}(\alpha,X_{Yw},X_{Dw}) , S_{2}=\frac{\partial M}{\partial \eta_{2}}(\alpha,X_{Yw},X_{Dw})\)
Demonstration 1:#
\(Given\ the\ general\ formula\,\ before\ using\ (\alpha,X_{Yw},X_{Dw}): \widetilde{Y}_{nx1}=Y_{nx1}-W_{nxp}\eta_{{{1}_{px1}}} ,\ \widetilde{D}_{nx1}=D_{nx1}-W_{nxp}\eta_{{{2}_{px1}}}: \\\ \\\ S_{1}=\frac{\partial M}{\partial \eta_{1}}|_{(\alpha,W_{Yw},W_{Dw})}\\\ \\\ =\frac{\partial E[(\widetilde{Y}_{nx1}(\eta_{1})-a\widetilde{D}(\eta_{2})_{nx1})'(\widetilde{D}(\eta_{2})_{nx1})}{\partial \eta_{1}}|_{(\alpha,W_{Yw},W_{Dw})}=\frac{\partial E[Y_{nx1}-W_{nxp}\eta_{{{1}_{px1}}}-aD_{nx1}+aW_{nxp}\eta_{{{2}_{px1}}})'(D_{nx1}-W_{nxp}\eta_{{{2}_{px1}}})}{\partial \eta_{1}}|_{(\alpha,W_{Yw},W_{Dw})}\\\ \\\ Substituting\ (\alpha,W_{Yw},W_{Dw})\ in\ (a,\eta_{1},\eta_{2})\\\ \\\ =\frac{\partial E[(\widetilde{Y}_{nx1}(\eta_{1})-a\widetilde{D}(\eta_{2})_{nx1})'(\widetilde{D}(\eta_{2})_{nx1})]}{\partial \eta_{1}}|_{(\alpha,W_{Yw},W_{Dw})}=E[(W_{nxp})'(D_{nx1}-W_{n*p}\eta_{{2}_{px1}})]|_{(\alpha,W_{Yw},W_{Dw})}\\ =E[(W_{nxp})'(D_{nx1}-W_{n*p}X_{{{Dw}_{px1}}})]\\ =E[W'_{pxn}D_{nx1}-W'_{pxn}W_{nxp}(W'_{pxn}W_{nxp})^{-1}(W'_{pxn}D_{nx1})]\\ =E[W'_{pxn}D_{nx1}-I_{pxp}(W'_{pxn}D_{nx1})]=E[W'_{pxn}D_{nx1}-W'_{pxn}D_{nx1}]=E[0]\\ S_{1}=0\)
Demonstration 2:#
\(Given\ the\ general\ formula\,\ before\ using\ (\alpha,X_{Yw},X_{Dw}): \widetilde{Y}_{nx1}=y_{nx1}-W_{nxp}\eta_{{{1}_{px1}}} ,\ \widetilde{D}_{nx1}=D_{nx1}-W_{nxp}\eta_{{{2}_{px1}}}\\\ \\\ S_{2}=\frac{\partial M}{\partial \eta_{2}}|_{(\alpha,W_{Yw},W_{Dw})}=0\\\ \\ =\frac{\partial E[(\widetilde{Y}_{nx1}(\eta_{1})-a\widetilde{D}(\eta_{2})_{nx1})'(\widetilde{D}(\eta_{2})_{nx1})}{\partial \eta_{2}}|_{(\alpha,W_{Yw},W_{Dw})}=\frac{\partial E[Y_{nx1}-W_{nxp}\eta_{{{1}_{px1}}}-aD_{nx1}+aW_{nxp}\eta_{{{2}_{px1}}})'(D_{nx1}-W_{nxp}\eta_{{{2}_{px1}}})}{\partial \eta_{2}}|_{(\alpha,W_{Yw},W_{Dw})}\\ =\frac{\partial E[-Y_{1xn}'W_{nxp}\eta_{{2}_{px1}}+\eta'_{{1}_{1xn}}W'_{pxn}W_{pxn}\eta_{{2}_{px1}}+aD'_{1xn}W_{nxp}\eta_{{2}_{px1}}+a\eta'_{{2}_{1xp}}W'_{pxn}D_{nx1}-a\eta'_{{2}_{1xp}}W'_{pxn}W_{nxp}\eta_{{2}_{px1}}]}{\partial \eta_{2}}|_{(\alpha,W_{Yw},W_{Dw})}\\ =E[-W'_{pxn}Y_{nx1}+W'_{pxn}W_{nxp}\eta_{{1}_{px1}}+aW'_{pxn}D_{nx1}+aW'_{pxn}D_{nx1}-aW'_{pxn}W_{nxp}\eta_{{2}_{px1}}-aW'_{pxn}W_{nxp}\eta_{{2}_{px1}}]|_{(\alpha,W_{Yw},W_{Dw})}\\\ \\\ Substituting\ (\alpha,W_{Yw},W_{Dw})\ in\ (a,\eta_{1},\eta_{2})\\\ \\ =E[-W'_{pxn}Y_{nx1}+W'_{pxn}W_{nxp}X_{{{yw}_{px1}}}+\alpha W'_{pxn}D_{nx1}+\alpha W'_{pxn}D_{nx1}-\alpha W'_{pxn}W_{nxp}X_{{{Dw}_{px1}}}-\alpha W'_{pxn}W_{nxp}X_{{{Dw}_{px1}}}]\\ =E[-W'_{pxn}Y_{nx1}+W'_{pxn}W_{nxp}(W'_{pxn}W_{nxp})^{-1}(W'_{pxn}Y_{nx1})+\alpha W'_{pxn}D_{nx1}+\alpha W'_{pxn}D_{nx1}-\alpha W'_{pxn}W_{nxp}(W'_{pxn}W_{nxp})^{-1}(W'_{pxn}D_{nx1})-\alpha W'_{pxn}W_{nxp}(W'_{pxn}W_{nxp})^{-1}(W'_{pxn}D_{nx1})]\\ =E[-W'_{pxn}Y_{nx1}+-W'_{pxn}Y_{nx1}+\alpha W'_{pxn}D_{nx1}+\alpha W'_{pxn}D_{nx1}-\alpha W'_{pxn}D_{nx1}-\alpha W'_{pxn}D_{nx1}]=E[0]=0\\ S_{2}=0\)
2. Code Section#
2.1. Orthogonal Learning#
using IJulia
using Distributions
using DataFrames
using CSV
using Tables
using GLM
using CovarianceMatrices
using Gadfly
using Statistics
using Markdown
include("../julia_notebooks/hdmjl/hdmjl.jl")
SystemError: opening file "C:\\Users\\Matias Villalba\\Documents\\GitHub\\CausalInferenceML\\labs\\julia_notebooks\\hdmjl\\hdmjl.jl": No such file or directory
Stacktrace:
[1] systemerror(p::String, errno::Int32; extrainfo::Nothing)
@ Base .\error.jl:176
[2] systemerror
@ .\error.jl:175 [inlined]
[3] open(fname::String; lock::Bool, read::Nothing, write::Nothing, create::Nothing, truncate::Nothing, append::Nothing)
@ Base .\iostream.jl:293
[4] open
@ .\iostream.jl:275 [inlined]
[5] open(f::Base.var"#433#434"{String}, args::String; kwargs::@Kwargs{})
@ Base .\io.jl:394
[6] open
@ .\io.jl:393 [inlined]
[7] read
@ .\io.jl:486 [inlined]
[8] _include(mapexpr::Function, mod::Module, _path::String)
@ Base .\loading.jl:2132
[9] include(fname::String)
@ Base.MainInclude .\client.jl:489
[10] top-level scope
@ In[2]:1
Simulation Design#
We are going to simulate 3 different trials to show the properties we talked about orthogonal learning.
For that we first define a function that runs a single observation of our simulation.
function simulate_once(seed)
Random.seed!(seed)
n = 100
p = 100
beta = 1 ./ (1:p) .^ 2 # Note the use of ./ for element-wise division
gamma = 1 ./ (1:p) .^ 2
X = rand(Normal(0, 1), n, p)
D = X * gamma .+ (rand(Normal(0, 1), n, 1) / 4) # Note the use of .+ for element-wise addition
Y = 10 * D .+ X * beta .+ rand(Normal(0, 1), n, 1) # Note the use of .+ for element-wise addition
X = DataFrame(X, :auto)
D = DataFrame(D, ["D"])
X1 = hcat(D, X)
Y = DataFrame(Y, ["Y"])
## NAIVE
model1=rlasso_arg( X1, Y ,nothing, true, true, true, false, false,
nothing, 1.1, nothing, 5000, 15, 10^(-5), -Inf, false, Inf, true )
coef1 = rlasso(model1)["coefficients"][3:102,2]
SX_IDs = findall(rlasso(model1)["coefficients"][3:102,2] .!= 0 )
if (sum(coef1[SX_IDs,:])==0)
Y1 = hcat(Y,D)
naive_coef = coef(lm(@formula(Y ~ D), Y1))[2]
end
if (sum(coef1[SX_IDs,:])>0)
Y2 = hcat(Y, D)
for i in 1:length(SX_IDs)
col_name = Symbol("X$SX_IDs[i]")
Y2[!, col_name] = X[!, SX_IDs[i]]
end
formula = Term(:Y) ~ Term(:D) + sum(Term(Symbol("X$SX_IDs[i]")) for i in 1:length(SX_IDs))
naive_coef = coef(lm(formula, Y2))[2]
end
model2 =rlasso_arg( X, Y ,nothing, true, true, true, false, false,
nothing, 1.1, nothing, 5000, 15, 10^(-5), -Inf, true, Inf, true )
model3 =rlasso_arg( X, D ,nothing, true, true, true, false, false,
nothing, 1.1, nothing, 5000, 15, 10^(-5), -Inf, true, Inf, true );
resY = rlasso(model2)["residuals"]
resD = rlasso(model3)["residuals"]
Y3=DataFrame(hcat(resY,resD),["resY","resD"])
orthogonal_coef = coef(lm(@formula(resY ~ resD), Y3))[2]
return naive_coef, orthogonal_coef
end
simulate_once (generic function with 1 method)
simulate_once(0)
(10.908754441475432, 9.991524145807752)
Then we define a function that runs the simulation on its enterity, using parallel computing and the function we previously defined.
function run_simulation(B)
results = pmap(simulate_once, 1:B)
Naive = [result[1] for result in results]
Orthogonal = [result[2] for result in results]
return Naive, Orthogonal
end
run_simulation (generic function with 1 method)
Orto_breaks = 8:0.2:12
Naive_breaks = 8:0.2:12
8.0:0.2:12.0
function create_histogram_data(data, breaks)
counts, edges = fit(Histogram, data, breaks).weights, breaks
midpoints = (edges[1:end-1] .+ edges[2:end]) ./ 2
return DataFrame(midpoints = midpoints, counts = counts ./ sum(counts) ./ 0.2) # Normalized to density
end
create_histogram_data (generic function with 1 method)
Next we run the simulations with 100, 1000, and 10000 iterations and plot the histograms for the Naive and Orthogonal estimations
Bs = [100, 1000, 10000]
for B in Bs
start_time = time()
Naive, Orthogonal = run_simulation(B)
end_time = time()
elapsed_time = end_time - start_time # Calculate elapsed time
naive_hist = create_histogram_data(Naive, Naive_breaks)
ortho_hist = create_histogram_data(Orthogonal, Orto_breaks)
naive_plot = plot(naive_hist,
x = :midpoints, y = :counts, Geom.bar,
Guide.xlabel("Estimated Effect"), Guide.ylabel("Density"),
Coord.cartesian(xmin=8, xmax=12),
Theme(default_color=color("lightblue"),
panel_fill=color("white"),
background_color=color("white")),
Guide.title("Naive estimation")
)
ortho_plot = plot(ortho_hist,
x = :midpoints, y = :counts, Geom.bar,
Guide.xlabel("Estimated Effect"), Guide.ylabel("Density"),
Coord.cartesian(xmin=8, xmax=12),
Theme(default_color=color("lightblue"),
panel_fill=color("white"),
background_color=color("white")),
Guide.title("Orthogonal estimation")
)
# Combine the plots side by side
combined_plot = hstack(ortho_plot, naive_plot)
# Display the title and combined plots in a Jupyter notebook
println("Time taken for $B iteration simulation: $(round(elapsed_time, digits=2)) seconds\n")
display("text/markdown","### Simulated with $B Iterations")
display(combined_plot)
end
Simulated with 100 Iterations
Time taken for 100 iteration simulation: 5.78 seconds
Time taken for 1000 iteration simulation: 56.9 seconds
Time taken for 10000 iteration simulation: 741.64 seconds
Simulated with 1000 Iterations
Simulated with 10000 Iterations
We can se that the orthogonal estimation yields on average a coeficient more centered on the true effect than the naive estimation. This method of estimation that utilizes the residuals of lasso regresion and helps reduce bias more efficiently than the naive estimation method. This is because it leverages the properties explained on the begining of this notebook rather than just controlling for a relevant set of covariates which may induce endogeneity.
We have used parallel computing because it is supposed to allow us to achieve better processing times. It can significantly lower the running time of computations due to its ability to distribute the workload across multiple processing units.
2.2. Double Lasso - Using School data#
#pkgs
using Pkg
Pkg.add("CSV")
Pkg.add("DataFrames")
Pkg.add("Statistics")
Pkg.add("Plots")
Pkg.add("StatsModels")
Pkg.add("Lasso")
Pkg.add("MLDataUtils")
Pkg.add("HDM")
Updating registry at `C:\Users\juanl\.julia\registries\General.toml`
Resolving package versions...
Installed WorkerUtilities ─ v1.6.1
Installed CSV ───────────── v0.10.14
Updating `C:\Users\juanl\.julia\environments\v1.10\Project.toml`
[336ed68f] + CSV v0.10.14
Updating `C:\Users\juanl\.julia\environments\v1.10\Manifest.toml`
[336ed68f] + CSV v0.10.14
[76eceee3] + WorkerUtilities v1.6.1
Precompiling project...
✓ UnPack
✓ WorkerUtilities
✓ BufferedStreams
✓ StructTypes
✓ NodeJS
✓ FillArrays
✓ GenericLinearAlgebra
✓ URIParser
✓ AliasTables
✓ Nullables
✓ StaticArraysCore
✓ Missings
✓ ReadOnlyArrays
✓ ProtoBuf
✓ ConstructionBase
✓ ZipFile
✓ DataValues
✓ Quadmath
✓ Latexify
✗ BinaryProvider
✓ DataStructures
✓ Parameters
✓ NodeJS_18_jll
✓ ReadStat_jll
✓ Electron
✓ WeakRefStrings
✓ EzXML
✓ FileIO
✓ OpenSSL
✗ PyCall
✓ Unitful → ConstructionBaseUnitfulExt
✓ Setfield
✓ SortingAlgorithms
✓ Thrift
✓ TableShowUtils
✓ TableTraitsUtils
✗ Snappy
✓ MemPool
✓ FillArrays → FillArraysPDMatsExt
✓ QuadGK
✓ FlatBuffers
✓ CategoricalArrays
✓ XLSX
✓ ReadStat
✓ QueryOperators
✓ DataTables
✓ StatsBase
✓ IterableTables
✓ HTTP
✗ ExcelReaders
✓ FillArrays → FillArraysStatisticsExt
✓ JSON3
✗ Parquet
✓ StatFiles
✓ StatsModels
✓ Arrow
✓ Query
✓ JSONSchema
✓ Vega
✓ FeatherLib
✗ ExcelFiles
✗ ParquetFiles
✓ Distributions
✓ CSV
✓ FeatherFiles
✓ Distributions → DistributionsTestExt
✓ VegaLite
✓ GLM
✓ Polynomials
✓ DataVoyager
✓ DoubleFloats
✓ TextParse
✓ CSVFiles
✓ DataFrames
✓ Latexify → DataFramesExt
✓ UnitfulLatexify
✗ Queryverse
✓ Plots
✓ Plots → FileIOExt
✓ Plots → UnitfulExt
✓ Plots → IJuliaExt
73 dependencies successfully precompiled in 160 seconds. 172 already precompiled.
8 dependencies errored.
For a report of the errors see `julia> err`. To retry use `pkg> precompile`
Resolving package versions...
No Changes to `C:\Users\juanl\.julia\environments\v1.10\Project.toml`
No Changes to `C:\Users\juanl\.julia\environments\v1.10\Manifest.toml`
Resolving package versions...
Updating `C:\Users\juanl\.julia\environments\v1.10\Project.toml`
[10745b16] + Statistics v1.10.0
No Changes to `C:\Users\juanl\.julia\environments\v1.10\Manifest.toml`
Resolving package versions...
No Changes to `C:\Users\juanl\.julia\environments\v1.10\Project.toml`
No Changes to `C:\Users\juanl\.julia\environments\v1.10\Manifest.toml`
Resolving package versions...
Updating `C:\Users\juanl\.julia\environments\v1.10\Project.toml`
[3eaba693] + StatsModels v0.7.3
No Changes to `C:\Users\juanl\.julia\environments\v1.10\Manifest.toml`
Resolving package versions...
Installed FFTW ──────────── v1.8.0
Installed MLBase ────────── v0.9.2
Installed MKL_jll ───────── v2024.1.0+0
Installed oneTBB_jll ────── v2021.12.0+0
Installed IntelOpenMP_jll ─ v2024.1.0+0
Installed DSP ───────────── v0.7.9
Installed AbstractFFTs ──── v1.5.0
Installed Lasso ─────────── v0.7.1
Installed FFTW_jll ──────── v3.3.10+0
Installed IterTools ─────── v1.10.0
Updating `C:\Users\juanl\.julia\environments\v1.10\Project.toml`
[b4fcebef] + Lasso v0.7.1
Updating `C:\Users\juanl\.julia\environments\v1.10\Manifest.toml`
[621f4979] + AbstractFFTs v1.5.0
[717857b8] + DSP v0.7.9
[7a1cc6ca] + FFTW v1.8.0
[c8e1da08] + IterTools v1.10.0
[b4fcebef] + Lasso v0.7.1
[f0e99cf1] + MLBase v0.9.2
[f5851436] + FFTW_jll v3.3.10+0
[1d5cc7b8] + IntelOpenMP_jll v2024.1.0+0
[856f044c] + MKL_jll v2024.1.0+0
[1317d2d5] + oneTBB_jll v2021.12.0+0
[4af54fe1] + LazyArtifacts
Precompiling project...
✓ AbstractFFTs
✓ IterTools
✓ IntelOpenMP_jll
✓ oneTBB_jll
✓ FFTW_jll
✓ AbstractFFTs → AbstractFFTsTestExt
✓ MLBase
MKL_jll Waiting for background task / IO / timer.
[pid 20180] waiting for IO to finish:
Handle type uv_handle_t->data
timer 0000019ca1299b50->0000019c9f177280
This means that a package has started a background task or event source that has not finished running. For precompilation to complete successfully, the event source needs to be closed explicitly. See the developer documentation on fixing precompilation hangs for more help.
[pid 20180] waiting for IO to finish:
Handle type uv_handle_t->data
timer 0000019ca1299b50->0000019c9f177280
This means that a package has started a background task or event source that has not finished running. For precompilation to complete successfully, the event source needs to be closed explicitly. See the developer documentation on fixing precompilation hangs for more help.
✓ MKL_jll
✓ FFTW
✓ Polynomials → PolynomialsFFTWExt
✓ DSP
✓ Lasso
12 dependencies successfully precompiled in 61 seconds. 246 already precompiled. 8 skipped during auto due to previous errors.
1 dependency had output during precompilation:
┌ MKL_jll
│ Downloading artifact: MKL
│
│ [pid 20180] waiting for IO to finish:
│ Handle type uv_handle_t->data
│ timer 0000019ca1299b50->0000019c9f177280
│ This means that a package has started a background task or event source that has not finished running. For precompilation to complete successfully, the event source needs to be closed explicitly. See the developer documentation on fixing precompilation hangs for more help.
│
│ [pid 20180] waiting for IO to finish:
│ Handle type uv_handle_t->data
│ timer 0000019ca1299b50->0000019c9f177280
│ This means that a package has started a background task or event source that has not finished running. For precompilation to complete successfully, the event source needs to be closed explicitly. See the developer documentation on fixing precompilation hangs for more help.
└
Resolving package versions...
Installed JpegTurbo_jll ─────── v3.0.3+0
Installed Libmount_jll ──────── v2.40.1+0
Installed GR_jll ────────────── v0.73.5+0
Installed Unitful ───────────── v1.19.1
Installed CEnum ─────────────── v0.4.2
Installed HTTP ──────────────── v1.10.8
Installed Xorg_libSM_jll ────── v1.2.4+0
Installed Fontconfig_jll ────── v2.13.96+0
Installed Libgpg_error_jll ──── v1.49.0+0
Installed SentinelArrays ────── v1.4.2
Installed LZO_jll ───────────── v2.10.2+0
Installed SpecialFunctions ──── v2.4.0
Installed TranscodingStreams ── v0.9.13
Installed Polynomials ───────── v4.0.8
Installed FriBidi_jll ───────── v1.0.14+0
Installed MappedArrays ──────── v0.4.2
Installed Compat ────────────── v4.15.0
Installed Xorg_libXext_jll ──── v1.3.6+0
Installed StatsBase ─────────── v0.33.21
Installed Colors ────────────── v0.12.11
Installed GR ────────────────── v0.73.5
Installed ZMQ ───────────────── v1.2.3
Installed ColorSchemes ──────── v3.25.0
Installed Expat_jll ─────────── v2.6.2+0
Installed Xorg_libXrender_jll ─ v0.9.11+0
Installed Parquet ───────────── v0.4.0
Installed Pixman_jll ────────── v0.43.4+0
Installed Libuuid_jll ───────── v2.40.1+0
Installed AliasTables ───────── v1.1.2
Installed Xorg_libICE_jll ───── v1.1.1+0
Installed MLDataUtils ───────── v0.5.4
Installed Libgcrypt_jll ─────── v1.8.11+0
Installed FixedPointNumbers ─── v0.8.5
Installed LAME_jll ──────────── v3.100.2+0
Installed FillArrays ────────── v1.11.0
Installed Glib_jll ──────────── v2.80.2+0
Installed LearnBase ─────────── v0.3.0
Installed MLLabelUtils ──────── v0.5.7
Installed MLDataPattern ─────── v0.5.4
Installed CodecZstd ─────────── v0.7.2
Updating `C:\Users\juanl\.julia\environments\v1.10\Project.toml`
[cc2ba9b6] + MLDataUtils v0.5.4
Updating `C:\Users\juanl\.julia\environments\v1.10\Manifest.toml`
[66dad0bd] ↑ AliasTables v1.0.0 ⇒ v1.1.2
⌅ [fa961155] + CEnum v0.4.2
⌅ [6b39b394] + CodecZstd v0.7.2
[35d6a980] ↑ ColorSchemes v3.24.0 ⇒ v3.25.0
[5ae59095] ↑ Colors v0.12.10 ⇒ v0.12.11
[34da2185] ↑ Compat v4.14.0 ⇒ v4.15.0
[1a297f60] ↑ FillArrays v1.10.1 ⇒ v1.11.0
[53c48c17] ↑ FixedPointNumbers v0.8.4 ⇒ v0.8.5
[28b8d3ca] ↑ GR v0.73.3 ⇒ v0.73.5
[cd3eb016] ↑ HTTP v1.10.6 ⇒ v1.10.8
⌅ [7f8f8fb0] + LearnBase v0.3.0
⌃ [9920b226] + MLDataPattern v0.5.4
[cc2ba9b6] + MLDataUtils v0.5.4
[66a33bbf] + MLLabelUtils v0.5.7
[dbb5928d] + MappedArrays v0.4.2
⌅ [626c502c] ↑ Parquet v0.3.2 ⇒ v0.4.0
[f27b6e38] ↑ Polynomials v4.0.7 ⇒ v4.0.8
[91c51154] ↑ SentinelArrays v1.4.1 ⇒ v1.4.2
[276daf66] ↑ SpecialFunctions v2.3.1 ⇒ v2.4.0
⌅ [2913bbd2] ↓ StatsBase v0.34.3 ⇒ v0.33.21
⌅ [3bb67fe8] ↓ TranscodingStreams v0.10.7 ⇒ v0.9.13
[1986cc42] ↑ Unitful v1.19.0 ⇒ v1.19.1
[c2297ded] ↑ ZMQ v1.2.2 ⇒ v1.2.3
[2e619515] ↑ Expat_jll v2.5.0+0 ⇒ v2.6.2+0
[a3f928ae] ↑ Fontconfig_jll v2.13.93+0 ⇒ v2.13.96+0
[559328eb] ↑ FriBidi_jll v1.0.10+0 ⇒ v1.0.14+0
[d2c73de3] ↑ GR_jll v0.73.3+0 ⇒ v0.73.5+0
[7746bdde] ↑ Glib_jll v2.80.0+0 ⇒ v2.80.2+0
[aacddb02] ↑ JpegTurbo_jll v3.0.2+0 ⇒ v3.0.3+0
[c1c5ebd0] ↑ LAME_jll v3.100.1+0 ⇒ v3.100.2+0
[dd4b983a] ↑ LZO_jll v2.10.1+0 ⇒ v2.10.2+0
[d4300ac3] ↑ Libgcrypt_jll v1.8.7+0 ⇒ v1.8.11+0
[7add5ba3] ↑ Libgpg_error_jll v1.42.0+0 ⇒ v1.49.0+0
[4b2f31a3] ↑ Libmount_jll v2.39.3+0 ⇒ v2.40.1+0
[38a345b3] ↑ Libuuid_jll v2.39.3+1 ⇒ v2.40.1+0
[30392449] ↑ Pixman_jll v0.42.2+0 ⇒ v0.43.4+0
[f67eecfb] ↑ Xorg_libICE_jll v1.0.10+1 ⇒ v1.1.1+0
[c834827a] ↑ Xorg_libSM_jll v1.2.3+0 ⇒ v1.2.4+0
[1082639a] ↑ Xorg_libXext_jll v1.3.4+4 ⇒ v1.3.6+0
[ea2f1a96] ↑ Xorg_libXrender_jll v0.9.10+4 ⇒ v0.9.11+0
Info Packages marked with ⌃ and ⌅ have new versions available. Those with ⌃ may be upgradable, but those with ⌅ are restricted by compatibility constraints from upgrading. To see why use `status --outdated -m`
Precompiling project...
✓ CEnum
✓ Compat
✓ AliasTables
✓ MappedArrays
✓ FillArrays
✓ Libmount_jll
✓ Xorg_libICE_jll
✓ TranscodingStreams
✓ LAME_jll
✓ SentinelArrays
✓ Pixman_jll
✓ JpegTurbo_jll
✓ Expat_jll
✓ LZO_jll
✓ Libgpg_error_jll
✓ Libuuid_jll
✓ FriBidi_jll
✓ Compat → CompatLinearAlgebraExt
✓ Glib_jll
✓ Xorg_libSM_jll
✓ CodecZlib
✓ Libtiff_jll
✓ CodecZstd
✓ ZMQ
✓ FixedPointNumbers
✓ Libgcrypt_jll
✓ FillArrays → FillArraysPDMatsExt
✓ Fontconfig_jll
✓ SpecialFunctions
✓ Quadmath
✓ FilePathsBase
✓ XSLT_jll
✓ DataStructures
✓ FillArrays → FillArraysStatisticsExt
✓ DualNumbers
✓ SortingAlgorithms
✓ Xorg_libXext_jll
✓ Xorg_libXrender_jll
✓ FilePaths
✓ ColorTypes
✓ HTTP
✓ QuadGK
✓ QueryOperators
✓ HypergeometricFunctions
✓ Cairo_jll
✓ Electron
✓ StatsBase
✓ Qt6Base_jll
✗ Parquet
✓ HarfBuzz_jll
✓ Vega
✓ LearnBase
✓ Query
✓ StatsFuns
✓ ColorVectorSpace
✓ Colors
✓ libass_jll
✓ MLBase
✓ MLLabelUtils
✓ ColorVectorSpace → SpecialFunctionsExt
✓ StatsModels
✓ FFMPEG_jll
✓ VegaLite
✓ FFMPEG
✓ MLDataPattern
✓ GR_jll
✓ Polynomials
✓ Unitful
✓ CSV
✓ Distributions
✓ Unitful → ConstructionBaseUnitfulExt
✓ ColorSchemes
✓ Polynomials → PolynomialsFFTWExt
✓ DataVoyager
✓ Distributions → DistributionsTestExt
✓ GR
✓ DoubleFloats
✓ GLM
✓ DSP
✓ Lasso
✓ PlotUtils
✓ TextParse
✓ PlotThemes
✓ CSVFiles
✓ RecipesPipeline
✓ DataFrames
✓ Latexify → DataFramesExt
✓ MLDataUtils
✓ UnitfulLatexify
✓ Plots
✓ Plots → FileIOExt
✓ Plots → UnitfulExt
✓ Plots → IJuliaExt
92 dependencies successfully precompiled in 202 seconds. 172 already precompiled. 7 skipped during auto due to previous errors.
1 dependency precompiled but a different version is currently loaded. Restart julia to access the new version
# Libraries
using CSV
using DataFrames
using Statistics
using Plots
using StatsModels
using Lasso
using MLDataUtils
using Random
using StatsBase
using GLM
using HDM
using LinearAlgebra
ArgumentError: Package HDM not found in current path.
- Run `import Pkg; Pkg.add("HDM")` to install the HDM package.
Stacktrace:
[1] macro expansion
@ .\loading.jl:1772 [inlined]
[2] macro expansion
@ .\lock.jl:267 [inlined]
[3] __require(into::Module, mod::Symbol)
@ Base .\loading.jl:1753
[4] #invoke_in_world#3
@ .\essentials.jl:926 [inlined]
[5] invoke_in_world
@ .\essentials.jl:923 [inlined]
[6] require(into::Module, mod::Symbol)
@ Base .\loading.jl:1746
# Read CSV file
df = CSV.read("./data/bruhn2016.csv", DataFrame)
| Row | outcome.test.score | treatment | school | is.female | mother.attended.secondary.school | father.attened.secondary.school | failed.at.least.one.school.year | family.receives.cash.transfer | has.computer.with.internet.at.home | is.unemployed | has.some.form.of.income | saves.money.for.future.purchases | intention.to.save.index | makes.list.of.expenses.every.month | negotiates.prices.or.payment.methods | financial.autonomy.index |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Float64 | Int64 | Int64 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | |
| 1 | 47.3674 | 0 | 17018390 | NA | NA | NA | NA | NA | NA | 1 | 1 | 0 | 29 | 0 | 1 | 52 |
| 2 | 58.1768 | 1 | 33002614 | NA | NA | NA | NA | NA | NA | 0 | 0 | 0 | 41 | 0 | 0 | 27 |
| 3 | 56.6717 | 1 | 35002914 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 48 | 0 | 1 | 56 |
| 4 | 29.0794 | 0 | 35908915 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 42 | 0 | 0 | 27 |
| 5 | 49.5635 | 1 | 33047324 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 50 | 0 | 1 | 31 |
| 6 | 43.0994 | 0 | 53012542 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 93 | 0 | 1 | 77 |
| 7 | 71.3296 | 0 | 53006984 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 52 | 0 | 1 | 43 |
| 8 | 80.0634 | 0 | 33049475 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 50 | 0 | 0 | 31 |
| 9 | 88.7516 | 1 | 35925639 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 59 | 0 | 1 | 50 |
| 10 | 61.4361 | 1 | 35008758 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 44 | 0 | 1 | 14 |
| 11 | 63.8114 | 1 | 35005307 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | NA | 0 | 1 | 73 |
| 12 | 66.0135 | 0 | 33024537 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 60 | 0 | 1 | 56 |
| 13 | 39.5818 | 1 | 33075212 | NA | NA | NA | NA | NA | NA | 1 | 1 | 0 | NA | 0 | 1 | 60 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 17288 | 35.0643 | 1 | 35012087 | 1 | 0 | NA | 1 | 1 | 1 | 1 | 1 | 0 | 31 | 0 | 0 | 41 |
| 17289 | 67.246 | 1 | 33081743 | 1 | 1 | NA | 0 | 0 | 1 | 0 | 0 | 1 | 96 | 0 | 1 | 60 |
| 17290 | 52.3272 | 1 | 33099243 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 60 | 0 | 0 | 52 |
| 17291 | 76.769 | 1 | 31069019 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 56 | 0 | 1 | 54 |
| 17292 | 62.9471 | 0 | 23174986 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 77 | 0 | 1 | 62 |
| 17293 | 67.1646 | 0 | 53012623 | NA | NA | NA | NA | NA | NA | 0 | 1 | 0 | 68 | 0 | 0 | 27 |
| 17294 | 60.3028 | 0 | 35038301 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 46 | 0 | 1 | NA |
| 17295 | 49.4898 | 1 | 35012178 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 34 | 0 | 1 | 43 |
| 17296 | 56.4573 | 0 | 35005320 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 15 | 0 | 0 | 35 |
| 17297 | 59.7006 | 0 | 33016070 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | NA | 0 | 41 | 0 | 0 | 24 |
| 17298 | 57.5156 | 0 | 53007514 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 79 | 0 | 1 | 46 |
| 17299 | 27.3903 | 1 | 33075212 | NA | NA | NA | NA | NA | NA | 1 | 1 | 0 | 57 | 0 | 0 | -9 |
first(df, 5)
| Row | outcome.test.score | treatment | school | is.female | mother.attended.secondary.school | father.attened.secondary.school | failed.at.least.one.school.year | family.receives.cash.transfer | has.computer.with.internet.at.home | is.unemployed | has.some.form.of.income | saves.money.for.future.purchases | intention.to.save.index | makes.list.of.expenses.every.month | negotiates.prices.or.payment.methods | financial.autonomy.index |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Float64 | Int64 | Int64 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | |
| 1 | 47.3674 | 0 | 17018390 | NA | NA | NA | NA | NA | NA | 1 | 1 | 0 | 29 | 0 | 1 | 52 |
| 2 | 58.1768 | 1 | 33002614 | NA | NA | NA | NA | NA | NA | 0 | 0 | 0 | 41 | 0 | 0 | 27 |
| 3 | 56.6717 | 1 | 35002914 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 48 | 0 | 1 | 56 |
| 4 | 29.0794 | 0 | 35908915 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 42 | 0 | 0 | 27 |
| 5 | 49.5635 | 1 | 33047324 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 50 | 0 | 1 | 31 |
# Drop rows with any missing values
dropmissing!(df)
| Row | outcome.test.score | treatment | school | is.female | mother.attended.secondary.school | father.attened.secondary.school | failed.at.least.one.school.year | family.receives.cash.transfer | has.computer.with.internet.at.home | is.unemployed | has.some.form.of.income | saves.money.for.future.purchases | intention.to.save.index | makes.list.of.expenses.every.month | negotiates.prices.or.payment.methods | financial.autonomy.index |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Float64 | Int64 | Int64 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | String3 | |
| 1 | 47.3674 | 0 | 17018390 | NA | NA | NA | NA | NA | NA | 1 | 1 | 0 | 29 | 0 | 1 | 52 |
| 2 | 58.1768 | 1 | 33002614 | NA | NA | NA | NA | NA | NA | 0 | 0 | 0 | 41 | 0 | 0 | 27 |
| 3 | 56.6717 | 1 | 35002914 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 48 | 0 | 1 | 56 |
| 4 | 29.0794 | 0 | 35908915 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 42 | 0 | 0 | 27 |
| 5 | 49.5635 | 1 | 33047324 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 50 | 0 | 1 | 31 |
| 6 | 43.0994 | 0 | 53012542 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 93 | 0 | 1 | 77 |
| 7 | 71.3296 | 0 | 53006984 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 52 | 0 | 1 | 43 |
| 8 | 80.0634 | 0 | 33049475 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 50 | 0 | 0 | 31 |
| 9 | 88.7516 | 1 | 35925639 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 59 | 0 | 1 | 50 |
| 10 | 61.4361 | 1 | 35008758 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 44 | 0 | 1 | 14 |
| 11 | 63.8114 | 1 | 35005307 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | NA | 0 | 1 | 73 |
| 12 | 66.0135 | 0 | 33024537 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 60 | 0 | 1 | 56 |
| 13 | 39.5818 | 1 | 33075212 | NA | NA | NA | NA | NA | NA | 1 | 1 | 0 | NA | 0 | 1 | 60 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 17288 | 35.0643 | 1 | 35012087 | 1 | 0 | NA | 1 | 1 | 1 | 1 | 1 | 0 | 31 | 0 | 0 | 41 |
| 17289 | 67.246 | 1 | 33081743 | 1 | 1 | NA | 0 | 0 | 1 | 0 | 0 | 1 | 96 | 0 | 1 | 60 |
| 17290 | 52.3272 | 1 | 33099243 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 60 | 0 | 0 | 52 |
| 17291 | 76.769 | 1 | 31069019 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 56 | 0 | 1 | 54 |
| 17292 | 62.9471 | 0 | 23174986 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 77 | 0 | 1 | 62 |
| 17293 | 67.1646 | 0 | 53012623 | NA | NA | NA | NA | NA | NA | 0 | 1 | 0 | 68 | 0 | 0 | 27 |
| 17294 | 60.3028 | 0 | 35038301 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 46 | 0 | 1 | NA |
| 17295 | 49.4898 | 1 | 35012178 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 34 | 0 | 1 | 43 |
| 17296 | 56.4573 | 0 | 35005320 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 15 | 0 | 0 | 35 |
| 17297 | 59.7006 | 0 | 33016070 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | NA | 0 | 41 | 0 | 0 | 24 |
| 17298 | 57.5156 | 0 | 53007514 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 79 | 0 | 1 | 46 |
| 17299 | 27.3903 | 1 | 33075212 | NA | NA | NA | NA | NA | NA | 1 | 1 | 0 | 57 | 0 | 0 | -9 |
column_names = names(df)
println(column_names)
["outcome.test.score", "treatment", "school", "is.female", "mother.attended.secondary.school", "father.attened.secondary.school", "failed.at.least.one.school.year", "family.receives.cash.transfer", "has.computer.with.internet.at.home", "is.unemployed", "has.some.form.of.income", "saves.money.for.future.purchases", "intention.to.save.index", "makes.list.of.expenses.every.month", "negotiates.prices.or.payment.methods", "financial.autonomy.index"]
# Define an array of dependent variable names
dependent_vars = ["outcome.test.score", "intention.to.save.index", "negotiates.prices.or.payment.methods",
"has.some.form.of.income", "makes.list.of.expenses.every.month", "financial.autonomy.index",
"saves.money.for.future.purchases", "is.unemployed"]
8-element Vector{String}:
"outcome.test.score"
"intention.to.save.index"
"negotiates.prices.or.payment.methods"
"has.some.form.of.income"
"makes.list.of.expenses.every.month"
"financial.autonomy.index"
"saves.money.for.future.purchases"
"is.unemployed"
For Lasso regressions, we split the data into train and test data, and standarize the covariates matrix
X = select(df, Not(dependent_vars)) # equivalent to df.drop in Python
y = select(df, dependent_vars)
# Train-test split
(X_train, X_test), (y_train, y_test) = splitobs((X, y), at = 0.8, shuffle = true, rng = MersenneTwister(42))
| Row | treatment | school | is.female | mother.attended.secondary.school | father.attened.secondary.school | failed.at.least.one.school.year | family.receives.cash.transfer | has.computer.with.internet.at.home |
|---|---|---|---|---|---|---|---|---|
| Int64 | Int64 | String3 | String3 | String3 | String3 | String3 | String3 | |
| 1 | 1 | 35012178 | 0 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 23077883 | 0 | 1 | 0 | 1 | 1 | 1 |
| 3 | 1 | 33050490 | 0 | 0 | 0 | 0 | 1 | 0 |
| 4 | 0 | 33104352 | 0 | 1 | 1 | 0 | 0 | 0 |
| 5 | 0 | 33006458 | 1 | 0 | 0 | 0 | 1 | 1 |
| 6 | 0 | 33044899 | NA | NA | NA | NA | NA | NA |
| 7 | 0 | 23071095 | 0 | 0 | 1 | 0 | 0 | 1 |
| 8 | 0 | 33054711 | NA | NA | NA | NA | NA | NA |
| 9 | 0 | 33093555 | 0 | 0 | 0 | 0 | 1 | 0 |
| 10 | 1 | 35039895 | 1 | 1 | 0 | 0 | 0 | 0 |
| 11 | 0 | 35012221 | 1 | 1 | 1 | 0 | 0 | 1 |
| 12 | 0 | 35046164 | 1 | 1 | 1 | 0 | 0 | 0 |
| 13 | 0 | 35006567 | 1 | 1 | 0 | 0 | 0 | 0 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 3449 | 1 | 35012178 | 1 | 1 | 0 | 0 | NA | 0 |
| 3450 | 1 | 31330566 | 0 | 0 | 0 | 0 | 1 | 1 |
| 3451 | 0 | 33085498 | 1 | 1 | 1 | 1 | 0 | 0 |
| 3452 | 1 | 33044961 | NA | NA | NA | NA | NA | NA |
| 3453 | 1 | 23224509 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3454 | 0 | 23002590 | 1 | 0 | 0 | 0 | 1 | 1 |
| 3455 | 1 | 35011496 | 0 | 0 | 0 | 0 | 1 | 0 |
| 3456 | 0 | 17046270 | 0 | 0 | 0 | 0 | 0 | 1 |
| 3457 | 0 | 35019653 | 1 | 0 | 0 | 0 | 0 | 0 |
| 3458 | 0 | 23080841 | 0 | 0 | 0 | 1 | 0 | 1 |
| 3459 | 0 | 33007420 | 1 | 1 | 0 | 0 | 0 | 0 |
| 3460 | 0 | 35901386 | 1 | 1 | 1 | 0 | 1 | 0 |
# Extracting and removing 'treatment' from X
T_train = X_train[:, :treatment]
T_test = X_test[:, :treatment]
select!(X_train, Not(:treatment))
select!(X_test, Not(:treatment))
Column 'treatment' not found in one or both DataFrames.
# Standardizing the data
# Fit and transform the training data
scaler = fit(StandardScaler, X_train)
X_train_scaled = transform(scaler, X_train)
X_test_scaled = transform(scaler, X_test)
MethodError: no method matching standardize(::SubDataFrame{DataFrame, DataFrames.Index, Vector{Int64}}; fit::Bool, center::Bool, scale::Bool)
Closest candidates are:
standardize(::Type{DT}, ::AbstractVecOrMat{<:Real}; kwargs...) where DT<:AbstractDataTransform
@ StatsBase C:\Users\juanl\.julia\packages\StatsBase\XgjIN\src\transformations.jl:366
Stacktrace:
[1] top-level scope
@ In[26]:2
X_scaled = vcat(X_train_scaled, X_test_scaled)
T = vcat(T_train, T_test)
UndefVarError: `X_train_scaled_df` not defined
Stacktrace:
[1] top-level scope
@ In[27]:2
2.2.2. Regressions#
a. OLS#
From 1 - 3 regression: measures treatment impact on student financial proficiency
From 4 - 6 regression: measures treatment impact on student savings behavior and attitudes
From 7 - 9 regression: measures treatment impact on student money management behavior and attitudes
From 10 - 12 regression: measures treatment impact on student entrepreneurship and work outcomes
# OLS regressions with "Student Financial Proficiency" as dependent variable
ols_score_1 = lm(@formula(outcome_test_score ~ treatment), df)
ols_score_2 = lm(@formula(outcome_test_score ~ treatment + school + failed_at_least_one_school_year), df)
ols_score_3 = lm(@formula(outcome_test_score ~ treatment + school + failed_at_least_one_school_year + is_female + mother_attended_secondary_school + father_attended_secondary_school + family_receives_cash_transfer + has_computer_with_internet_at_home), df)
# OLS regressions with "Intention to save index" as dependent variable
ols_saving_1 = lm(@formula(intention_to_save_index ~ treatment), df)
ols_saving_2 = lm(@formula(intention_to_save_index ~ treatment + school + failed_at_least_one_school_year), df)
ols_saving_3 = lm(@formula(intention_to_save_index ~ treatment + school + failed_at_least_one_school_year + is_female + mother_attended_secondary_school + father_attended_secondary_school + family_receives_cash_transfer + has_computer_with_internet_at_home), df)
# OLS regressions with "Negotiates prices or payment methods" as dependent variable
ols_negotiates_1 = lm(@formula(negotiates_prices_or_payment_methods ~ treatment), df)
ols_negotiates_2 = lm(@formula(negotiates_prices_or_payment_methods ~ treatment + school + failed_at_least_one_school_year), df)
ols_negotiates_3 = lm(@formula(negotiates_prices_or_payment_methods ~ treatment + school + failed_at_least_one_school_year + is_female + mother_attended_secondary_school + father_attended_secondary_school + family_receives_cash_transfer + has_computer_with_internet_at_home), df)
# OLS regressions with "Has some form of income" as dependent variable
ols_manage_1 = lm(@formula(has_some_form_of_income ~ treatment), df)
ols_manage_2 = lm(@formula(has_some_form_of_income ~ treatment + school + failed_at_least_one_school_year), df)
ols_manage_3 = lm(@formula(has_some_form_of_income ~ treatment + school + failed_at_least_one_school_year + is_female + mother_attended_secondary_school + father_attended_secondary_school + family_receives_cash_transfer + has_computer_with_internet_at_home), df)
# show parameters in table
println(summary(ols_score_1))
println(summary(ols_score_2))
println(summary(ols_score_3))
# Save the ITT beta and the confidence intervals
beta_OLS = coef(ols_score_3)[coefnames(ols_score_3) .== "treatment"][1]
conf_int_OLS = confint(ols_score_3)[coefnames(ols_score_3) .== "treatment", :]
b. Double Lasso using cross validation#
Dependent var 1: Student Financial Proficiency
Step 1: We ran Lasso regression of Y (student financial proficiency) on X, and T on X
# For the outcome test score
lasso_model_y = glmnet(X_train_scaled, y_train.outcome_test_score; alpha=1)
cv_y = glmnetcv(X_train_scaled, y_train.outcome_test_score; alpha=1, nfolds=10)
best_lambda_y = cv_y.lambda_min
@printf "Best lambda for Y: %.4f\n" best_lambda_y
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Mejor lambda: 0.0001
# Predict Y using all X_scaled with the best lambda found
y_pred_yX = predict(lasso_model_y, X_scaled; lambda=best_lambda_y
# For the treatment variable
lasso_model_t = glmnet(X_train_scaled, T_train; alpha = 1)
cv_t = glmnetcv(X_train_scaled, T_train, alpha = 1, nfolds = 10)
best_lambda_t = cv_t.lambda_min
@printf "Best lambda for T: %.4f\n" best_lambda_t
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Mejor lambda: 0.0011
# Predicting T using all X_scaled
y_pred_TX = predict(lasso_model_t, X_scaled; lambda = best_lambda_t)
Step 2: Obtain the resulting residuals
res_yX = y[:, :outcome_test_score] - y_pred_yX
res_TX = T - y_pred_TX
Step 3: We run the least squares of res_yX on res_TX
ols_score = lm(@formula(res_yX ~ res_TX), regression_df)
# Printing the summary of the model directly
println("OLS Regression Results:")
println(coeftable(ols_score))
ArgumentError: Package PrettyTables not found in current path, maybe you meant `import/using .PrettyTables`.
- Otherwise, run `import Pkg; Pkg.add("PrettyTables")` to install the PrettyTables package.
Stacktrace:
[1] macro expansion
@ .\loading.jl:1772 [inlined]
[2] macro expansion
@ .\lock.jl:267 [inlined]
[3] __require(into::Module, mod::Symbol)
@ Base .\loading.jl:1753
[4] #invoke_in_world#3
@ .\essentials.jl:926 [inlined]
[5] invoke_in_world
@ .\essentials.jl:923 [inlined]
[6] require(into::Module, mod::Symbol)
@ Base .\loading.jl:1746
ols_score = sm.OLS.from_formula('res_yX ~ res_TX', data=df).fit()
# Show parameters in table
st = Stargazer([ols_score])
st
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
| Dependent variable: res_yX | |
| (1) | |
| Intercept | 0.033 |
| (0.126) | |
| res_TX | 4.324*** |
| (0.253) | |
| Observations | 12222 |
| R2 | 0.023 |
| Adjusted R2 | 0.023 |
| Residual Std. Error | 13.945 (df=12220) |
| F Statistic | 292.956*** (df=1; 12220) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 |
# Save the ITT beta and the confidence intervals
beta_DL_CV = coeff(ols_score, :res_TX)
conf_int_DL_CV = confint(ols_score)[2, :]
c. Double Lasso using theoretical lambda#
export RLasso, fit!, predict, lasso_model
struct RLasso
post::Bool
beta::Vector{Float64}
intercept::Float64
end
function RLasso(;post::Bool=true)
new(post, Float64[], 0.0)
end
function fit!(model::RLasso, X, y)
result = HDM.rlasso(X, y; post=model.post)
model.beta = result.beta
model.intercept = result.intercept
return model
end
function predict(model::RLasso, X)
return X * model.beta + model.intercept
end
lasso_model() = RLasso(post=false)
end
using .MyLasso
Step 1:
# Estimate y predictions with all X
y_pred_yX = predict_with_model(X_scaled, y[:, :outcome_test_score])
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
# Estimate T predictions with all X
y_pred_TX = predict_with_model(X_scaled, T)
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
Step 2:
res_yX = y[:, :outcome_test_score] - y_pred_yX
res_TX = T - y_pred_TX
df = DataFrame(res_yX = res_yX, res_TX = res_TX)
Step 3:
lasso_hdm_score = lm(@formula(res_yX ~ res_TX), df)
# Show parameters in table
println(coef(lasso_hdm_score))
Intel MKL WARNING: Support of Intel(R) Streaming SIMD Extensions 4.2 (Intel(R) SSE4.2) enabled only processors has been deprecated. Intel oneAPI Math Kernel Library 2025.0 will require Intel(R) Advanced Vector Extensions (Intel(R) AVX) instructions.
| Dependent variable: res_yX | |
| (1) | |
| Intercept | 0.000 |
| (0.126) | |
| res_TX | 4.316*** |
| (0.253) | |
| Observations | 12222 |
| R2 | 0.023 |
| Adjusted R2 | 0.023 |
| Residual Std. Error | 13.953 (df=12220) |
| F Statistic | 291.837*** (df=1; 12220) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 |
beta_DL_theo = coef(lasso_hdm_score)[2]
conf_int_DL_theo = confint(lasso_hdm_score)
d. Double Lasso using partialling out method#
rlasso_results = rlassoEffect(X_scaled, y[:, :outcome_test_score], T, method="partialling_out")
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[1], line 1
----> 1 rlassoEffect = hdmpy.rlassoEffect(X_scaled, y['outcome.test.score'], T, method='partialling out')
NameError: name 'hdmpy' is not defined
println(rlassoResults)
{'alpha': 4.313441,
'se': array([0.25271166]),
't': array([17.06862565]),
'pval': array([2.54111627e-65]),
'coefficients': 4.313441,
'coefficient': 4.313441,
'coefficients_reg': 0
(Intercept) 59.769260
x0 0.000000
x1 1.511205
x2 0.529423
x3 0.461196
x4 -2.878027
x5 -0.857569
x6 0.000000,
'selection_index': array([[False],
[ True],
[ True],
[ True],
[ True],
[ True],
[False]]),
'residuals': {'epsilon': array([[-10.04200277],
[-31.30841071],
[-15.13769394],
...,
[-17.22383794],
[ -3.93047339],
[ -4.88461742]]),
'v': array([[ 0.48682705],
[-0.513173 ],
[ 0.48682705],
...,
[ 0.48682705],
[-0.513173 ],
[-0.513173 ]], dtype=float32)},
'samplesize': 12222}
beta_part_out = rlasso_results.coef
se_part_out = rlasso_results.se
critical_value = 1.96 # For 95% confidence level
conf_int_part_out = (beta_part_out - critical_value * se_part_out, beta_part_out + critical_value * se_part_out)
Results#
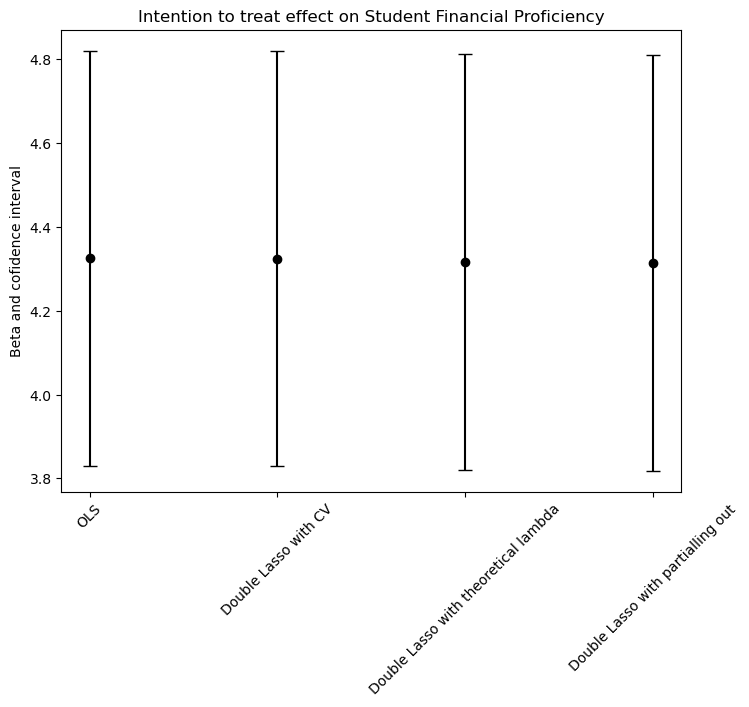
We found that the intention to treat effect (ITT) is very similar estimating with all 4 models (aproximately 4.3, with 95% of confidence). This could be because the ratio between the parameters and the number of observations p/n is small (8/12222 = 0.00065455735). In other words, we are not dealing with high dimensional data and the models from b. to d. will outperform the OLS when we are in the opposite scenario. In conclusion, we can say that the OLS model estimates the ITT just as good as the other models.
# Data preparation
methods = ["OLS", "Double Lasso with CV", "Double Lasso with theoretical lambda", "Double Lasso with partialling out"]
betas = [beta_OLS, beta_DL_CV, beta_DL_theo, beta_part_out]
lower_errors = [beta_OLS - conf_int_OLS[1], beta_DL_CV - conf_int_DL_CV[1], beta_DL_theo - conf_int_DL_theo[1], beta_part_out - conf_int_part_out[1]]
upper_errors = [conf_int_OLS[2] - beta_OLS, conf_int_DL_CV[2] - beta_DL_CV, conf_int_DL_theo[2] - beta_DL_theo, conf_int_part_out[2] - beta_part_out]
# Plotting
plt = plot(size=(800, 600), legend=false)
for (i, method) in enumerate(methods)
scatter!([i], [betas[i]], label=false, color="black")
plot!([i, i], [betas[i] - lower_errors[i], betas[i] + upper_errors[i]], color="black", label=false)
end
xticks!(1:length(methods), methods)
title!("Intention to treat effect on Student Financial Proficiency")
ylabel!("Beta and confidence interval")
xrotation!(45)
# Display the plot
display(plt)