Lab 5 - Python Code#
Authors: Valerie Dube, Erzo Garay, Juan Marcos Guerrero y Matias Villalba
Replication and Data analysis#
# Libraries
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import statsmodels.api as sm
import statsmodels.formula.api as smf
import hdmpy as hdm
from sklearn.base import BaseEstimator
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import KFold, cross_val_predict
from sklearn.linear_model import LassoCV, Lasso
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import GradientBoostingRegressor, RandomForestRegressor
1. Descriptives#
1.1. Descriptive table#
# Import data and see first observations
df = pd.read_csv("../../data/processed_esti.csv")
df.head()
| y | w | gender_female | gender_male | gender_transgender | ethnicgrp_asian | ethnicgrp_black | ethnicgrp_mixed_multiple | ethnicgrp_other | ethnicgrp_white | partners1 | postlaunch | msm | age | imd_decile | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 27 | 5 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 19 | 6 |
| 2 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 26 | 4 |
| 3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 20 | 2 |
| 4 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 24 | 3 |
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1739 entries, 0 to 1738
Data columns (total 15 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 y 1739 non-null int64
1 w 1739 non-null int64
2 gender_female 1739 non-null int64
3 gender_male 1739 non-null int64
4 gender_transgender 1739 non-null int64
5 ethnicgrp_asian 1739 non-null int64
6 ethnicgrp_black 1739 non-null int64
7 ethnicgrp_mixed_multiple 1739 non-null int64
8 ethnicgrp_other 1739 non-null int64
9 ethnicgrp_white 1739 non-null int64
10 partners1 1739 non-null int64
11 postlaunch 1739 non-null int64
12 msm 1739 non-null int64
13 age 1739 non-null int64
14 imd_decile 1739 non-null int64
dtypes: int64(15)
memory usage: 203.9 KB
control = df[df['w'] == 0].drop('y', axis=1)
treatment = df[df['w'] == 1].drop('y', axis=1)
def get_descriptive_stats(group, column):
if column == 'age':
count = group[column].count()
else:
count = (group[column] == 1).sum()
mean = group[column].mean()
std = group[column].std()
return count, mean, std
variables = df.columns.drop(['w', 'y'])
control_stats = {var: get_descriptive_stats(control, var) for var in variables}
treatment_stats = {var: get_descriptive_stats(treatment, var) for var in variables}
control_df = pd.DataFrame(control_stats, index=['count', 'mean', 'std']).T
treatment_df = pd.DataFrame(treatment_stats, index=['count', 'mean', 'std']).T
control_df.columns = pd.MultiIndex.from_product([['Control'], control_df.columns])
treatment_df.columns = pd.MultiIndex.from_product([['Treatment'], treatment_df.columns])
combined_df = pd.concat([control_df, treatment_df], axis=1)
formatted_table = combined_df[['Control', 'Treatment']].round(2)
print("Table 1: Descriptive Statistics and Balance\n")
print(formatted_table)
Table 1: Descriptive Statistics and Balance
Control Treatment
count mean std count mean std
gender_female 475.0 0.58 0.49 541.0 0.59 0.49
gender_male 342.0 0.42 0.49 377.0 0.41 0.49
gender_transgender 1.0 0.00 0.03 3.0 0.00 0.06
ethnicgrp_asian 45.0 0.06 0.23 66.0 0.07 0.26
ethnicgrp_black 76.0 0.09 0.29 74.0 0.08 0.27
ethnicgrp_mixed_multiple 76.0 0.09 0.29 78.0 0.08 0.28
ethnicgrp_other 14.0 0.02 0.13 9.0 0.01 0.10
ethnicgrp_white 607.0 0.74 0.44 694.0 0.75 0.43
partners1 239.0 0.29 0.46 277.0 0.30 0.46
postlaunch 387.0 0.47 0.50 512.0 0.56 0.50
msm 113.0 0.14 0.35 114.0 0.12 0.33
age 818.0 23.05 3.59 921.0 23.16 3.54
imd_decile 37.0 3.48 1.49 36.0 3.46 1.47
The observations for each variable are generally balanced between the control and treatment groups. Additionally, most participants are white, with an average age of approximately 23. The mean IMD decile scores are around 3.5, indicating that participants in both groups tend to come from more deprived areas.
1.2. Descriptive graphs#
ax = sns.barplot(
data=df.groupby('w')['gender_male'].value_counts(normalize=True).to_frame().set_axis(['prop'], axis=1),
x="gender_male",
y="prop",
hue="w",
)
ax.yaxis.set_major_formatter("{x:.0%}")
ax.set_xlabel("Gender (male=1, female or transgender=0)")
ax.legend(title='')
new_labels = ['Control', 'Treatment'] # Replace with your desired labels
for t, l in zip(ax.get_legend().texts, new_labels):
t.set_text(l)
plt.show()
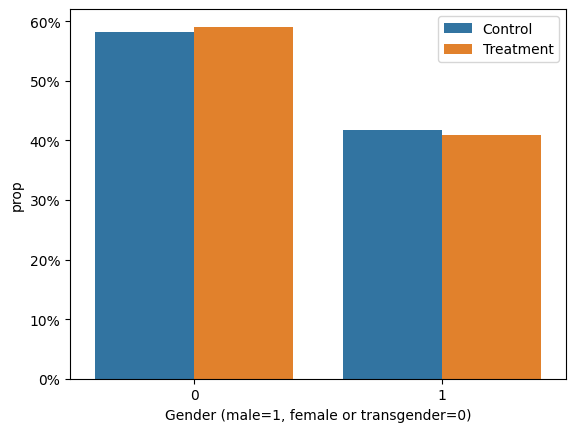
As we saw in section 1.1., there is a similar percentage of males and females participants in each treatment group in the sample.
ax = sns.barplot(
data=df.groupby('w')['partners1'].value_counts(normalize=True).to_frame().set_axis(['prop'], axis=1),
x="partners1",
y="prop",
hue="w",
)
ax.yaxis.set_major_formatter("{x:.0%}")
ax.set_xlabel("Number of partners (one partner=1)")
ax.legend(title='')
new_labels = ['Control', 'Treatment'] # Replace with your desired labels
for t, l in zip(ax.get_legend().texts, new_labels):
t.set_text(l)
plt.show()
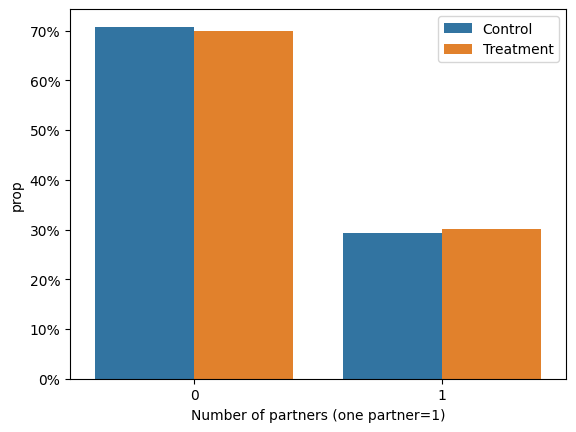
In a similar manner, we note an equal percentage of participants with 2 or more sexual partners as well as those with 1 sexual partner in the last 12 months from the beginning of the study, per treatment or control group.
ax = sns.histplot(data=df, x="age", hue="w", element="poly", stat="percent", common_norm=False)
new_labels = ['Control', 'Treatment'] # Replace with your desired labels
for t, l in zip(ax.get_legend().texts, new_labels):
t.set_text(l)
plt.show()
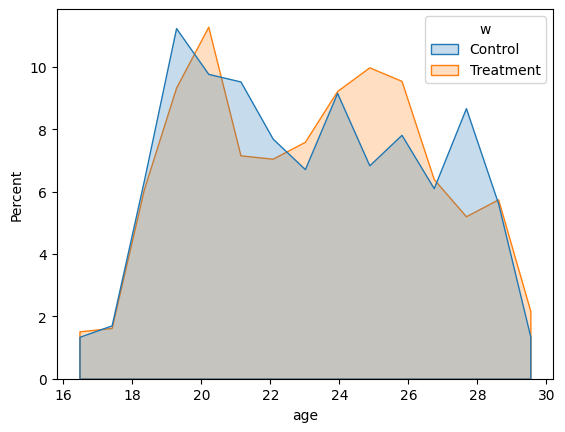
We can see a higher percentage of participants aged between 23 and 27 in the treatment group. Also, there is a higher perceptange of participants aged between 21 and 22 and 27 and 29 in the control group.
ax = sns.histplot(data=df, x="imd_decile", hue="w", element="poly", discrete=True, stat="percent", common_norm=False)
new_labels = ['Control', 'Treatment'] # Replace with your desired labels
for t, l in zip(ax.get_legend().texts, new_labels):
t.set_text(l)
plt.show()
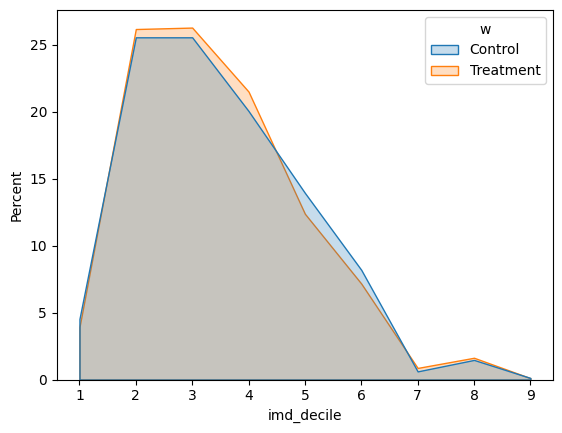
In the case of the IMD decile, an index that measures poverty in the UK, we can see the same proportion of participants in each group.
2. Linear Regression analysis#
2.1. Regression 1: \(y = \beta_0 + \beta_1 T + \epsilon\)#
model_1 = "y ~ w"
est_1 = smf.ols(formula=model_1 , data=df).fit()
print(est_1.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.077
Model: OLS Adj. R-squared: 0.076
Method: Least Squares F-statistic: 144.5
Date: Wed, 07 Aug 2024 Prob (F-statistic): 4.96e-32
Time: 21:44:28 Log-Likelihood: -1112.9
No. Observations: 1739 AIC: 2230.
Df Residuals: 1737 BIC: 2241.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.2115 0.016 13.174 0.000 0.180 0.243
w 0.2652 0.022 12.021 0.000 0.222 0.308
==============================================================================
Omnibus: 38241.926 Durbin-Watson: 1.995
Prob(Omnibus): 0.000 Jarque-Bera (JB): 217.327
Skew: 0.532 Prob(JB): 6.43e-48
Kurtosis: 1.634 Cond. No. 2.69
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
We found that the adjusted R-squared is 0.076 and the ATE is approximately 0.27. This means that the treatment explains only 7.6% of the increase in the STI tests between the control and treatment groups. Additionally, receiving the treatment (i.e. being invited to use the internet-based sexual health service) increases, on average, the probability of taking an STI test by 26.5%.
2.2. Regression 2: \(y = \beta_0 + \beta_1 T + \beta_2 X + \epsilon\)#
model_2 = "y ~ w + age + gender_female + ethnicgrp_white + ethnicgrp_black + ethnicgrp_mixed_multiple + partners1 + imd_decile + msm"
est_2 = smf.ols(formula=model_2 , data=df).fit()
print(est_2.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.107
Model: OLS Adj. R-squared: 0.102
Method: Least Squares F-statistic: 22.94
Date: Wed, 07 Aug 2024 Prob (F-statistic): 3.06e-37
Time: 21:44:28 Log-Likelihood: -1084.3
No. Observations: 1739 AIC: 2189.
Df Residuals: 1729 BIC: 2243.
Df Model: 9
Covariance Type: nonrobust
============================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------------------
Intercept -0.1807 0.088 -2.042 0.041 -0.354 -0.007
w 0.2622 0.022 12.044 0.000 0.220 0.305
age 0.0149 0.003 4.787 0.000 0.009 0.021
gender_female 0.0905 0.025 3.629 0.000 0.042 0.139
ethnicgrp_white 0.0499 0.041 1.209 0.227 -0.031 0.131
ethnicgrp_black -0.0292 0.054 -0.538 0.591 -0.136 0.077
ethnicgrp_mixed_multiple -0.0315 0.054 -0.587 0.557 -0.137 0.074
partners1 -0.0661 0.024 -2.714 0.007 -0.114 -0.018
imd_decile -0.0045 0.007 -0.609 0.543 -0.019 0.010
msm 0.0033 0.037 0.089 0.929 -0.069 0.075
==============================================================================
Omnibus: 2495.421 Durbin-Watson: 1.997
Prob(Omnibus): 0.000 Jarque-Bera (JB): 193.943
Skew: 0.524 Prob(JB): 7.69e-43
Kurtosis: 1.743 Cond. No. 215.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Compared to the previous regression, when we include additional variables (age, gender, ethnic group, number of sexual partners, the indicator for Randomised after SH:24 made publicly available, the indicator for men who have sex with men, and the socioeconomic level measured by deciles), we observe an increase in the adjusted R-squared of approximately 0.3 percentage points (from 0.1). Additionally, the ATE decreases by 0.003 percentage points, indicating a negative bias.
It is worth mentioning that we omit gender_male to avoid collinearity with gender_female. Similarly, we exclude the less relevant ethnic group (i.e. the one with fewer observations) to prevent the same issue.
2.3. Regression 3: \(y = \beta_0 + \beta_1 T + \beta_2 X + \epsilon\) (Double Lasso variable selection)#
# Assuming df is already defined
X = df[["gender_female", "ethnicgrp_white", "ethnicgrp_black", "gender_transgender", "msm", "partners1", "age", "imd_decile"]]
w = df['w']
y = df['y']
# Fit LassoCV model to find the optimal alpha (lambda)
cv_model3a = LassoCV(alphas=None, cv=10, max_iter=10000).fit(X, w)
cv_model3b = LassoCV(alphas=None, cv=10, max_iter=10000).fit(X, y)
# Fit Lasso model with the optimal alpha
model3a = Lasso(alpha=cv_model3a.alpha_).fit(X, w)
model3b = Lasso(alpha=cv_model3b.alpha_).fit(X, y)
# Identify non-zero coefficients from Lasso models
significant_vars3a = X.columns[model3a.coef_ != 0]
significant_vars3b = X.columns[model3b.coef_ != 0]
# Combine the significant variables from both models
significant_vars = pd.Index(np.unique(significant_vars3a.append(significant_vars3b)))
# Extract the significant variables for regression
X_significant = X[significant_vars]
# Add 'w' to the significant variables
X_significant_with_w = X_significant.copy()
X_significant_with_w['w'] = w
# Add constant term for intercept in the new significant variable set
X_significant_with_w = sm.add_constant(X_significant_with_w)
# Fit linear regression model on significant variables plus 'w' against 'y'
model3 = sm.OLS(y, X_significant_with_w).fit()
# Print summary of the model
print("Summary for the final model with dependent variable 'y':")
print(model3.summary())
Summary for the final model with dependent variable 'y':
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.106
Model: OLS Adj. R-squared: 0.103
Method: Least Squares F-statistic: 34.38
Date: Wed, 07 Aug 2024 Prob (F-statistic): 2.06e-39
Time: 21:44:28 Log-Likelihood: -1084.5
No. Observations: 1739 AIC: 2183.
Df Residuals: 1732 BIC: 2221.
Df Model: 6
Covariance Type: nonrobust
===================================================================================
coef std err t P>|t| [0.025 0.975]
-----------------------------------------------------------------------------------
const -0.2026 0.081 -2.508 0.012 -0.361 -0.044
age 0.0149 0.003 4.824 0.000 0.009 0.021
ethnicgrp_white 0.0710 0.025 2.805 0.005 0.021 0.121
gender_female 0.0888 0.022 3.977 0.000 0.045 0.133
imd_decile -0.0042 0.007 -0.569 0.570 -0.019 0.010
partners1 -0.0660 0.024 -2.725 0.006 -0.114 -0.019
w 0.2626 0.022 12.078 0.000 0.220 0.305
==============================================================================
Omnibus: 2501.289 Durbin-Watson: 1.996
Prob(Omnibus): 0.000 Jarque-Bera (JB): 194.167
Skew: 0.524 Prob(JB): 6.87e-43
Kurtosis: 1.743 Cond. No. 177.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
We observe that the ATE using double lasso is akin to the OLS with confounders, along with the adjusted R-squared.
2.4. Coefficient Comparison#
# Assuming model1, model2, model3 are your fitted statsmodels regression models
# Extract the coefficients for resW
b1 = est_1.params['w']
b2 = est_2.params['w']
b3 = model3.params['w']
# Extract the standard errors for resW
se1 = est_1.bse['w']
se2 = est_2.bse['w']
se3 = model3.bse['w']
# Labels for the models
model_labels = ['OLS', 'OLS w. controls', 'Double Lasso']
# Coefficients and standard errors
coefficients = [b1, b2, b3]
errors = [se1, se2, se3]
# Create the figure and axis
fig, ax = plt.subplots()
# Plot the coefficients with error bars
ax.errorbar(model_labels, coefficients, yerr=errors, fmt='o', capsize=5, capthick=2, marker='s', markersize=7, linestyle='None')
# Add title and labels
ax.set_title('Comparison of Coefficients from Different Models')
ax.set_xlabel('Model')
ax.set_ylabel('Coefficient')
# Add grid for better readability
ax.grid(True)
# Show the plot
plt.show()
C:\Users\Matias Villalba\AppData\Local\Temp\ipykernel_10508\2861833790.py:23: UserWarning: marker is redundantly defined by the 'marker' keyword argument and the fmt string "o" (-> marker='o'). The keyword argument will take precedence.
ax.errorbar(model_labels, coefficients, yerr=errors, fmt='o', capsize=5, capthick=2, marker='s', markersize=7, linestyle='None')
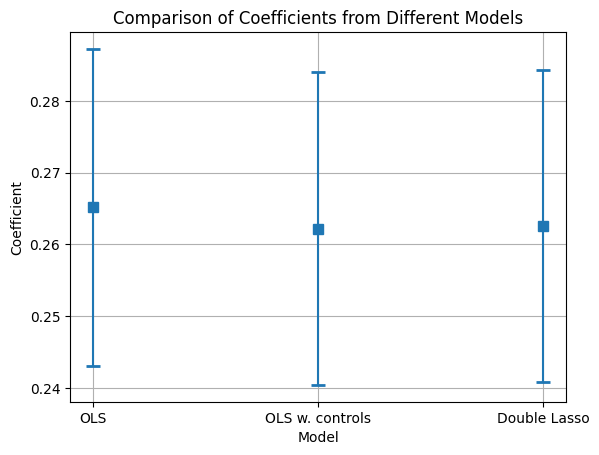
In general, the three ATEs are very similar, but we consider that the models that include the cofounders (OLS with controls and DL) are better estimated.
3. Non-Linear Methods DML#
def dml(X, D, y, modely, modeld, *, nfolds, classifier=False, time = None, clu = None, cluster = True):
cv = KFold(n_splits=nfolds, shuffle=True, random_state=123) # shuffled k-folds
yhat = cross_val_predict(modely, X, y, cv=cv, n_jobs=-1) # out-of-fold predictions for y
# out-of-fold predictions for D
# use predict or predict_proba dependent on classifier or regressor for D
if classifier:
Dhat = cross_val_predict(modeld, X, D, cv=cv, method='predict_proba', n_jobs=-1)[:, 1]
else:
Dhat = cross_val_predict(modeld, X, D, cv=cv, n_jobs=-1)
# calculate outcome and treatment residuals
resy = y - yhat
resD = D - Dhat
if cluster:
# final stage ols clustered
dml_data = pd.concat([clu, pd.Series(time), pd.Series(resy, name = 'resy'), pd.Series(resD, name = 'resD')], axis=1)
else:
# final stage ols nonclustered
dml_data = pd.concat([pd.Series(resy, name = 'resy'), pd.Series(resD, name = 'resD')], axis=1)
if cluster:
# clustered standard errors
ols_mod = smf.ols(formula = 'resy ~ 1 + resD', data = dml_data).fit(cov_type='cluster', cov_kwds={"groups": dml_data['CountyCode']})
else:
# regular ols
ols_mod = smf.ols(formula = 'resy ~ 1 + resD', data = dml_data).fit()
point = ols_mod.params[1]
stderr = ols_mod.bse[1]
epsilon = ols_mod.resid
return point, stderr, yhat, Dhat, resy, resD, epsilon
def summary(point, stderr, yhat, Dhat, resy, resD, epsilon, X, D, y, *, name):
'''
Convenience summary function that takes the results of the DML function
and summarizes several estimation quantities and performance metrics.
'''
return pd.DataFrame({'estimate': point, # point estimate
'stderr': stderr, # standard error
'lower': point - 1.96*stderr, # lower end of 95% confidence interval
'upper': point + 1.96*stderr, # upper end of 95% confidence interval
'rmse y': np.sqrt(np.mean(resy**2)), # RMSE of model that predicts outcome y
'rmse D': np.sqrt(np.mean(resD**2)) # RMSE of model that predicts treatment D
}, index=[name])
df['intercept'] = 1
y = df["y"]
d = df["w"]
x = df[df.columns[~df.columns.isin(['y','w'])]]
3.1. DML with RLasso#
class RLasso(BaseEstimator):
def __init__(self, *, post=True):
self.post = post
def fit(self, X, y):
self.rlasso_ = hdmpy.rlasso(X, y, post=self.post)
return self
def predict(self, X):
return np.array(X) @ np.array(self.rlasso_.est['beta']).flatten() + np.array(self.rlasso_.est['intercept'])
lasso_model = lambda: RLasso(post=False)
# DML with RLasso:
modely = make_pipeline(StandardScaler(), RLasso(post=False))
modeld = make_pipeline(StandardScaler(), RLasso(post=False))
result_RLasso = dml(x,d,y, modely, modeld, nfolds=10, classifier=False, cluster = False)
table_RLasso = summary(*result_RLasso, x,d,y, name = 'Lasso')
print(table_RLasso)
---------------------------------------------------------------------------
_RemoteTraceback Traceback (most recent call last)
_RemoteTraceback:
"""
Traceback (most recent call last):
File "C:\Users\Matias Villalba\AppData\Local\Programs\Python\Python312\Lib\site-packages\joblib\externals\loky\process_executor.py", line 463, in _process_worker
r = call_item()
^^^^^^^^^^^
File "C:\Users\Matias Villalba\AppData\Local\Programs\Python\Python312\Lib\site-packages\joblib\externals\loky\process_executor.py", line 291, in __call__
return self.fn(*self.args, **self.kwargs)
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
File "C:\Users\Matias Villalba\AppData\Local\Programs\Python\Python312\Lib\site-packages\joblib\parallel.py", line 598, in __call__
return [func(*args, **kwargs)
^^^^^^^^^^^^^^^^^^^^^
File "C:\Users\Matias Villalba\AppData\Local\Programs\Python\Python312\Lib\site-packages\sklearn\utils\parallel.py", line 129, in __call__
return self.function(*args, **kwargs)
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
File "C:\Users\Matias Villalba\AppData\Local\Programs\Python\Python312\Lib\site-packages\sklearn\model_selection\_validation.py", line 1378, in _fit_and_predict
estimator.fit(X_train, y_train, **fit_params)
File "C:\Users\Matias Villalba\AppData\Local\Programs\Python\Python312\Lib\site-packages\sklearn\base.py", line 1474, in wrapper
return fit_method(estimator, *args, **kwargs)
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
File "C:\Users\Matias Villalba\AppData\Local\Programs\Python\Python312\Lib\site-packages\sklearn\pipeline.py", line 475, in fit
self._final_estimator.fit(Xt, y, **last_step_params["fit"])
File "C:\Users\Matias Villalba\AppData\Local\Temp\ipykernel_10508\3396256270.py", line 7, in fit
NameError: name 'hdmpy' is not defined
"""
The above exception was the direct cause of the following exception:
NameError Traceback (most recent call last)
Cell In[19], line 4
2 modely = make_pipeline(StandardScaler(), RLasso(post=False))
3 modeld = make_pipeline(StandardScaler(), RLasso(post=False))
----> 4 result_RLasso = dml(x,d,y, modely, modeld, nfolds=10, classifier=False, cluster = False)
5 table_RLasso = summary(*result_RLasso, x,d,y, name = 'Lasso')
6 print(table_RLasso)
Cell In[15], line 3, in dml(X, D, y, modely, modeld, nfolds, classifier, time, clu, cluster)
1 def dml(X, D, y, modely, modeld, *, nfolds, classifier=False, time = None, clu = None, cluster = True):
2 cv = KFold(n_splits=nfolds, shuffle=True, random_state=123) # shuffled k-folds
----> 3 yhat = cross_val_predict(modely, X, y, cv=cv, n_jobs=-1) # out-of-fold predictions for y
4 # out-of-fold predictions for D
5 # use predict or predict_proba dependent on classifier or regressor for D
6 if classifier:
File ~\AppData\Local\Programs\Python\Python312\Lib\site-packages\sklearn\utils\_param_validation.py:213, in validate_params.<locals>.decorator.<locals>.wrapper(*args, **kwargs)
207 try:
208 with config_context(
209 skip_parameter_validation=(
210 prefer_skip_nested_validation or global_skip_validation
211 )
212 ):
--> 213 return func(*args, **kwargs)
214 except InvalidParameterError as e:
215 # When the function is just a wrapper around an estimator, we allow
216 # the function to delegate validation to the estimator, but we replace
217 # the name of the estimator by the name of the function in the error
218 # message to avoid confusion.
219 msg = re.sub(
220 r"parameter of \w+ must be",
221 f"parameter of {func.__qualname__} must be",
222 str(e),
223 )
File ~\AppData\Local\Programs\Python\Python312\Lib\site-packages\sklearn\model_selection\_validation.py:1293, in cross_val_predict(estimator, X, y, groups, cv, n_jobs, verbose, fit_params, params, pre_dispatch, method)
1290 # We clone the estimator to make sure that all the folds are
1291 # independent, and that it is pickle-able.
1292 parallel = Parallel(n_jobs=n_jobs, verbose=verbose, pre_dispatch=pre_dispatch)
-> 1293 predictions = parallel(
1294 delayed(_fit_and_predict)(
1295 clone(estimator),
1296 X,
1297 y,
1298 train,
1299 test,
1300 routed_params.estimator.fit,
1301 method,
1302 )
1303 for train, test in splits
1304 )
1306 inv_test_indices = np.empty(len(test_indices), dtype=int)
1307 inv_test_indices[test_indices] = np.arange(len(test_indices))
File ~\AppData\Local\Programs\Python\Python312\Lib\site-packages\sklearn\utils\parallel.py:67, in Parallel.__call__(self, iterable)
62 config = get_config()
63 iterable_with_config = (
64 (_with_config(delayed_func, config), args, kwargs)
65 for delayed_func, args, kwargs in iterable
66 )
---> 67 return super().__call__(iterable_with_config)
File ~\AppData\Local\Programs\Python\Python312\Lib\site-packages\joblib\parallel.py:2007, in Parallel.__call__(self, iterable)
2001 # The first item from the output is blank, but it makes the interpreter
2002 # progress until it enters the Try/Except block of the generator and
2003 # reach the first `yield` statement. This starts the aynchronous
2004 # dispatch of the tasks to the workers.
2005 next(output)
-> 2007 return output if self.return_generator else list(output)
File ~\AppData\Local\Programs\Python\Python312\Lib\site-packages\joblib\parallel.py:1650, in Parallel._get_outputs(self, iterator, pre_dispatch)
1647 yield
1649 with self._backend.retrieval_context():
-> 1650 yield from self._retrieve()
1652 except GeneratorExit:
1653 # The generator has been garbage collected before being fully
1654 # consumed. This aborts the remaining tasks if possible and warn
1655 # the user if necessary.
1656 self._exception = True
File ~\AppData\Local\Programs\Python\Python312\Lib\site-packages\joblib\parallel.py:1754, in Parallel._retrieve(self)
1747 while self._wait_retrieval():
1748
1749 # If the callback thread of a worker has signaled that its task
1750 # triggered an exception, or if the retrieval loop has raised an
1751 # exception (e.g. `GeneratorExit`), exit the loop and surface the
1752 # worker traceback.
1753 if self._aborting:
-> 1754 self._raise_error_fast()
1755 break
1757 # If the next job is not ready for retrieval yet, we just wait for
1758 # async callbacks to progress.
File ~\AppData\Local\Programs\Python\Python312\Lib\site-packages\joblib\parallel.py:1789, in Parallel._raise_error_fast(self)
1785 # If this error job exists, immediatly raise the error by
1786 # calling get_result. This job might not exists if abort has been
1787 # called directly or if the generator is gc'ed.
1788 if error_job is not None:
-> 1789 error_job.get_result(self.timeout)
File ~\AppData\Local\Programs\Python\Python312\Lib\site-packages\joblib\parallel.py:745, in BatchCompletionCallBack.get_result(self, timeout)
739 backend = self.parallel._backend
741 if backend.supports_retrieve_callback:
742 # We assume that the result has already been retrieved by the
743 # callback thread, and is stored internally. It's just waiting to
744 # be returned.
--> 745 return self._return_or_raise()
747 # For other backends, the main thread needs to run the retrieval step.
748 try:
File ~\AppData\Local\Programs\Python\Python312\Lib\site-packages\joblib\parallel.py:763, in BatchCompletionCallBack._return_or_raise(self)
761 try:
762 if self.status == TASK_ERROR:
--> 763 raise self._result
764 return self._result
765 finally:
NameError: name 'hdmpy' is not defined
The message treatment providing information about Internet-accessed sexually transmitted infection testing predicts an increase in the probability that a person will get tested by 25.91 percentage points compared to receiving information about nearby clinics offering in-person testing. By providing both groups with information about testing, we mitigate the potential reminder effect, as both groups are equally prompted to consider testing. This approach allows us to isolate the impact of the type of information “Internet-accessed testing” versus “in-person clinic testing” on the likelihood of getting tested. Through randomized assignment, we establish causality rather than mere correlation, confirming that the intervention’s effect is driven by the unique advantages of Internet-accessed testing, such as increased privacy, reduced embarrassment, and convenience
3.2. DML with Regression Trees#
modely = make_pipeline(StandardScaler(), DecisionTreeRegressor(ccp_alpha=0.001, min_samples_leaf=5, random_state=123))
modeld = make_pipeline(StandardScaler(), DecisionTreeRegressor(ccp_alpha=0.001, min_samples_leaf=5, random_state=123))
result_RT = dml(x,d,y, modely, modeld, nfolds=10, classifier=False, cluster = False)
table_RT= summary(*result_RT, x,d,y, name = 'RT')
print(table_RT)
estimate stderr lower upper rmse y rmse D
RT 0.249831 0.021872 0.206961 0.292701 0.472259 0.499638
C:\Users\Matias Villalba\AppData\Local\Temp\ipykernel_23460\2498640246.py:30: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
point = ols_mod.params[1]
C:\Users\Matias Villalba\AppData\Local\Temp\ipykernel_23460\2498640246.py:31: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
stderr = ols_mod.bse[1]
The message treatment providing information about Internet-accessed sexually transmitted infection testing predicts an increase in the probability that a person will get tested by 24.98 percentage points compared to receiving information about nearby clinics offering in-person testing. By providing both groups with information about testing, we mitigate the potential reminder effect, as both groups are equally prompted to consider testing. This approach allows us to isolate the impact of the type of information “Internet-accessed testing” versus “in-person clinic testing” on the likelihood of getting tested. Through randomized assignment, we establish causality rather than mere correlation, confirming that the intervention’s effect is driven by the unique advantages of Internet-accessed testing, such as increased privacy, reduced embarrassment, and convenience
3.3. DML Boosting Trees#
modely = make_pipeline(StandardScaler(), GradientBoostingRegressor(n_estimators=100, max_depth=3, random_state=123))
modeld = make_pipeline(StandardScaler(), GradientBoostingRegressor(n_estimators=100, max_depth=3, random_state=123))
result_GBT = dml(x,d,y, modely, modeld, nfolds=10, classifier=False, cluster = False)
table_GBT = summary(*result_GBT, x,d,y, name = 'GBT')
print(table_GBT)
estimate stderr lower upper rmse y rmse D
GBT 0.246373 0.021669 0.203902 0.288843 0.475893 0.508383
C:\Users\Matias Villalba\AppData\Local\Temp\ipykernel_23460\2498640246.py:30: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
point = ols_mod.params[1]
C:\Users\Matias Villalba\AppData\Local\Temp\ipykernel_23460\2498640246.py:31: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
stderr = ols_mod.bse[1]
The message treatment providing information about Internet-accessed sexually transmitted infection testing predicts an increase in the probability that a person will get tested by 24.64 percentage points compared to receiving information about nearby clinics offering in-person testing. By providing both groups with information about testing, we mitigate the potential reminder effect, as both groups are equally prompted to consider testing. This approach allows us to isolate the impact of the type of information “Internet-accessed testing” versus “in-person clinic testing” on the likelihood of getting tested. Through randomized assignment, we establish causality rather than mere correlation, confirming that the intervention’s effect is driven by the unique advantages of Internet-accessed testing, such as increased privacy, reduced embarrassment, and convenience
3.4. DML with Random Forest#
modely = make_pipeline(StandardScaler(), RandomForestRegressor(n_estimators=100, min_samples_leaf=5, random_state=123))
modeld = make_pipeline(StandardScaler(), RandomForestRegressor(n_estimators=100, min_samples_leaf=5, random_state=123))
result_RF = dml(x,d,y, modely, modeld, nfolds=10, classifier=False, cluster = False)
table_RF = summary(*result_RF, x,d,y, name = 'RF')
print(table_RF)
estimate stderr lower upper rmse y rmse D
RF 0.241558 0.021379 0.199655 0.283461 0.472297 0.511585
C:\Users\Matias Villalba\AppData\Local\Temp\ipykernel_23460\2498640246.py:30: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
point = ols_mod.params[1]
C:\Users\Matias Villalba\AppData\Local\Temp\ipykernel_23460\2498640246.py:31: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
stderr = ols_mod.bse[1]
The message treatment providing information about Internet-accessed sexually transmitted infection testing predicts an increase in the probability that a person will get tested by 24.16 percentage points compared to receiving information about nearby clinics offering in-person testing. By providing both groups with information about testing, we mitigate the potential reminder effect, as both groups are equally prompted to consider testing. This approach allows us to isolate the impact of the type of information “Internet-accessed testing” versus “in-person clinic testing” on the likelihood of getting tested. Through randomized assignment, we establish causality rather than mere correlation, confirming that the intervention’s effect is driven by the unique advantages of Internet-accessed testing, such as increased privacy, reduced embarrassment, and convenience
3.6.#
# Extract coefficients and standard errors
coefficients = [result_RLasso[0], result_RT[0], result_GBT[0], result_RF[0]]
standard_errors = [result_RLasso[1], result_RT[1], result_GBT[1], result_RF[1]]
methods = ['RLasso', 'Regression Trees', 'Boosting Trees', 'Regression Forest']
# Plotting the coefficients with error bars
plt.figure(figsize=(10, 6))
plt.errorbar(methods, coefficients, yerr=standard_errors, fmt='o', capsize=5, capthick=2)
plt.xlabel('Regression Methods')
plt.ylabel('Coefficients')
plt.title('Comparison of Coefficients Across Regression Methods')
plt.grid(True)
plt.show()
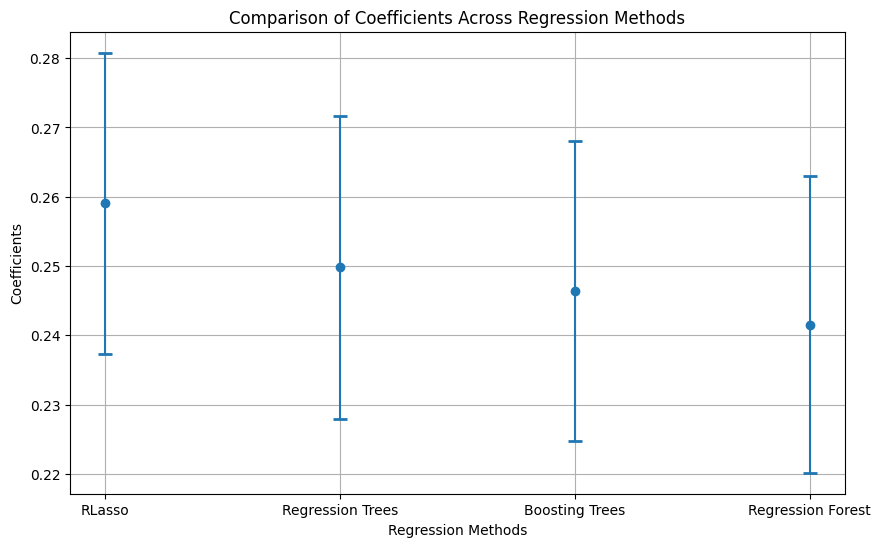
results_table = pd.concat([table_RLasso, table_RT, table_GBT, table_RF], axis=0)
print(results_table)
estimate stderr lower upper rmse y rmse D
Lasso 0.259067 0.021722 0.216492 0.301642 0.471041 0.500225
RT 0.249831 0.021872 0.206961 0.292701 0.472259 0.499638
GBT 0.246373 0.021669 0.203902 0.288843 0.475893 0.508383
RF 0.241558 0.021379 0.199655 0.283461 0.472297 0.511585
To choose the best model, we must compare the RMSEs of the outcome variable Y. In this case, the model with the lowest RMSE for Y is generated by Lasso (0.471041), whereas the lowest for the treatment is generated by Regression Trees (0.4983734). Therefore, DML could be employed with Y cleaned using Lasso and the treatment using Regression Trees.